PLANETCALC Онлайн калькуляторы

Войти
УчебаМатематикаГеометрия

Деление круга на равные части

Статья содержит два калькулятора, рассчитывающие параметры деления круга на равные по площади части радиусами и параллельными хордами

Эта страница существует благодаря следующим персонам

Timur

Timur

A

Anton

Создан: 2020-10-14 13:12:17, Последнее изменение: 2020-11-03 14:19:41
Creative Commons Attribution/Share-Alike License 3.0 (Unported)

Этот материал распространяется на условиях лицензии Creative Commons Attribution/Share-Alike License 3.0 (Unported). Это означает, что вы можете размещать этот контент на своем сайте или создавать на его основе собственный (в том числе и в коммерческих целях), при условии сохранения оригинального лицензионного соглашения. Кроме того, Вы должны отметить автора этой работы, путем размещения HTML ссылки на оригинал работы https://planetcalc.ru/8943/. Пожалуйста оставьте без изменения все ссылки на других авторов данной работы или работы, на основе которой создана данная работа (если таковые имеются в спроводительном тексте).

Ниже представлены два калькулятора, рассчитывающие параметры разделения круга на равные части. Сначала - традиционный калькулятор, который делит круг на равные части радиусами (примерно так, как режут пиццу или торт), под ним - нетрадиционный калькулятор, который делит круг на равные по площади части параллельными хордами. Оба калькулятора визуализируют результат рисунком. Методы расчета с формулами для обоих калькуляторов приведены ниже, под калькуляторами.

PLANETCALC, Деление круга на равные по площади части радиусами

Деление круга на равные по площади части радиусами

Знаков после запятой: 2
Угол сектора
 
Длина дуги
 
Длина хорды
 

PLANETCALC, Деление круга на равные по площади части параллельными хордами

Деление круга на равные по площади части параллельными хордами

Знаков после запятой: 2
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.

Деление круга на равные части радиусами

Традиционный и очень простой метод деления круга - по факту, нарезка равных секторов. Метод и формулы очень просты:

  1. Определяем угловой размер каждого сектора в радианах, путем деления 360 градусов на нужное число секторов.

\alpha=\frac{2\pi}{N}

  1. Определяем размер дуги сектора, перемножая радиус на угол в радианах

a=\alpha R

  1. Определяем размер хорды по теореме косинусов (хорда является основанием равнобедренного треугольника с боковыми сторонами R и противолежащим углом альфа.

c=R^2+R^2-2RR \cos \alpha

Собственно и всё - мы получили все характеристики для N равных секторов

Деление круга на равные части параллельными хордами

Этот способ более любопытен, чем предыдущий. Для простоты будем рассматривать верхнюю половину круга, так как с нижней все будет симметрично.

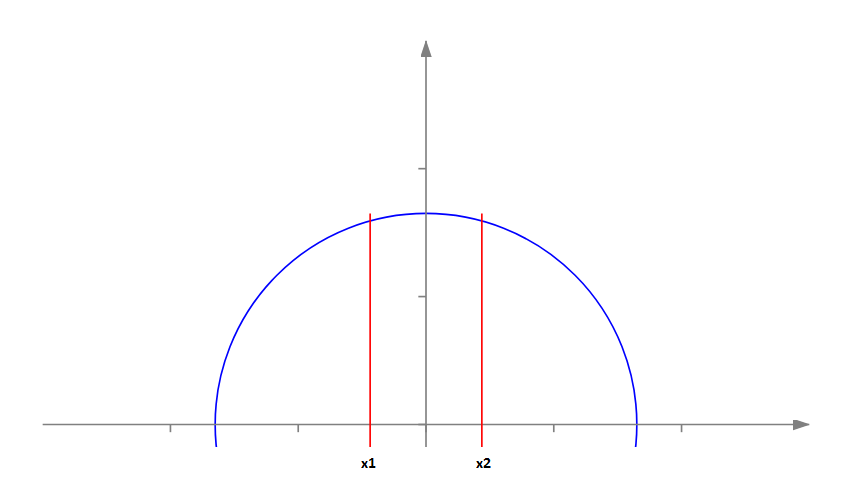
Деление круга на три равные части двумя хордами
Деление круга на три равные части двумя хордами

Задача состоит в определении x-вой координаты точек, через которые нужно проводить хорды (на рисунке это точки x1 и x2). Выведем для начала формулу площади куска, отсекаемого хордой слева.

Верхнюю полуокружность можно представить графиком функции y=f(x), где x - это координата вдоль оси абсцисс, а y - это функция, численно равная y координате соответствующей точки верхней полуокружности.

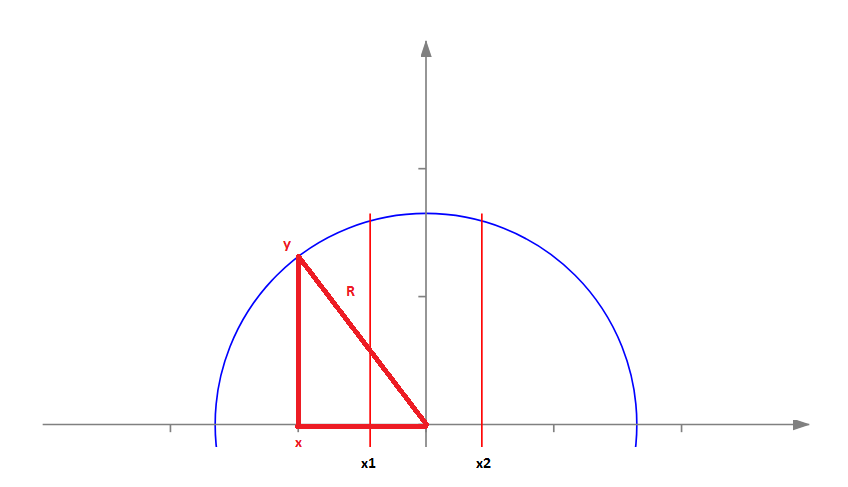
y=f(x)
y=f(x)

По теореме Пифагора получаем следующую функцию

y=\sqrt{R^2 - x^2}}

Чтобы получить площадь фигуры, отсекаемой хордой слева, надо проинтегрировать эту функцию от -R до x. Первообразная функции равна:

F(x)=\frac{1}{2} (x\sqrt{R^2-x^2} + R^2 \arctan(\frac{x}{\sqrt{R^2-x^2}}))+C

Осталось определиться с константой. Нам надо, чтобы в точке с координатами -R площадь была равна нулю. Подставив -R вместо x в формулу выше, получаем

F(-R)=-\frac{\pi R^2}{4}+C=0, откуда

C=\frac{\pi R^2}{4}

Итак, полное выражение
F(x)=\frac{1}{2} (x\sqrt{R^2-x^2} + R^2 \arctan(\frac{x}{\sqrt{R^2-x^2}}))+\frac{\pi R^2}{4}

Теперь рассмотрим нахождение координат крайней левой точки. Нам известна площадь, которую она должна отсечь (напоминаю, речь идет о полуокружности)

S=\frac{\frac{\pi R^2}{2}}{N}=\frac{\pi R^2}{2N}

Таким образом мы можем приравнять

\frac{1}{2} (x\sqrt{R^2-x^2} + R^2 \arctan(\frac{x}{\sqrt{R^2-x^2}}))+\frac{\pi R^2}{4}=\frac{\pi R^2}{2N}

Что дает нам такое финальное уравнение

\frac{1}{2} (x\sqrt{R^2-x^2} + R^2 \arctan(\frac{x}{\sqrt{R^2-x^2}}))+\frac{\pi R^2}{4}-\frac{\pi R^2}{2N}=0

Данное уравнение является трансцендентным, а поэтому находить координату первой точки придется численным методом, например, методом бисекции или методом Ньютона. Калькулятор использует метод Ньютона.

Вторая и последующие точки находится аналогично, путем изменения размера отсекаемой площади. Для второй точки это будет S_2=2\frac{\pi R^2}{2N}, для третьей S_3=3\frac{\pi R^2}{2N} и так далее.

Зная координаты точек, несложно рассчитать все остальные параметры, в частности, длину хорды.

Ссылка скопирована в буфер обмена

Похожие калькуляторы

 #геометрия #круг Геометрия круг окружность площадь радиус сектор угол хорда
PLANETCALC, Деление круга на равные части
Timur2020-11-03 14:19:41

Комментарии