Метод Ньютона
Этот онлайн калькулятор ищет корень (нуль) заданной функции, используя метод Ньютона (также известный как метод касательных)
Этот онлайн калькулятор применяет метод Ньютона (также известный как метод касательных) используя калькулятор производных для получения аналитической формулы производной заданной функции (метод Ньютона требует вычисления производной). Под калькулятором можно прочитать краткое описание метода.
Метод Ньютона1
Метод Ньютона, алгоритм Ньютона (также известный как метод касательных) — это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643—1727). Поиск решения осуществляется путём построения последовательных приближений и основан на принципах простой итерации.
Основная идея метода заключается в следующем: задаётся начальное приближение вблизи предположительного корня, после чего строится касательная к графику исследуемой функции в точке приближения, для которой находится пересечение с осью абсцисс. Эта точка берётся в качестве следующего приближения. Далее процесс повторяется, пока не будет достигнута необходимая точность.
Уравнение касательной к графику функции выглядит следующим образом:
,
где - тангенс угла пересечения касательной с осью абсцисс.
Тангенс угла пересечения касательной с осью абсцисс, - не что иное, как значение производной в точке
.
С учетом того факта, что в точке пересечения с осью абсцисс значение y равно нулю, можно записать следующее выражение для нахождения точки пересечения (следующей точки приближения):
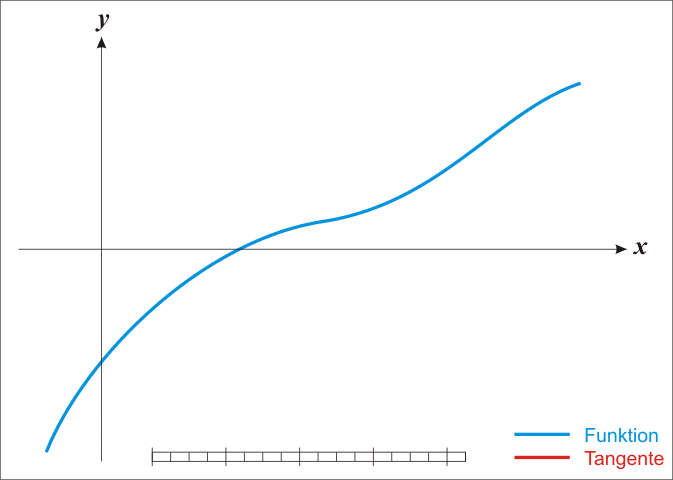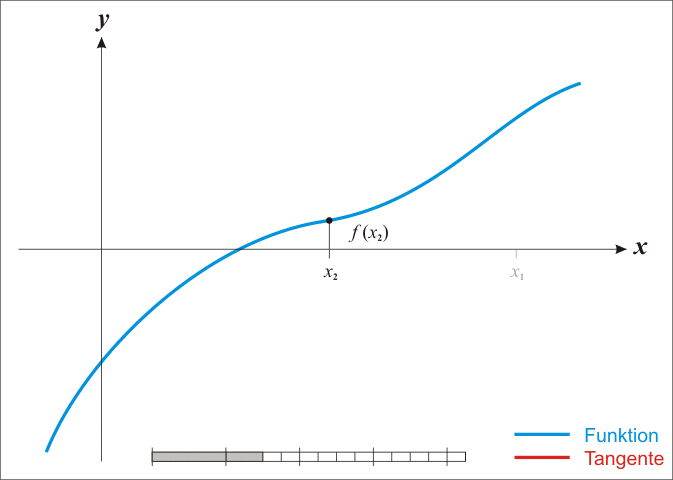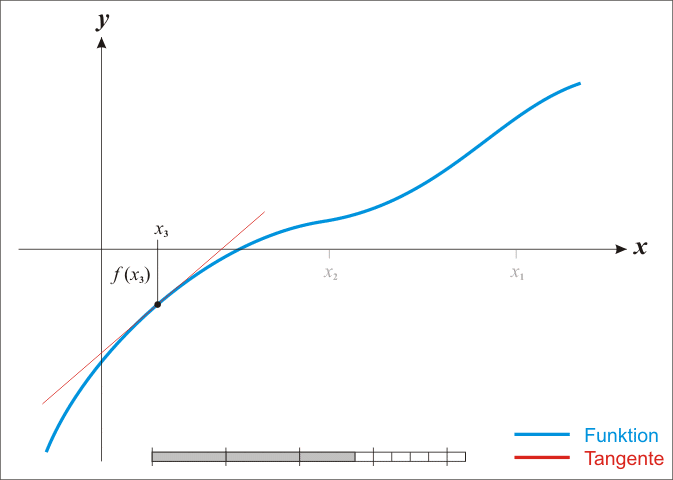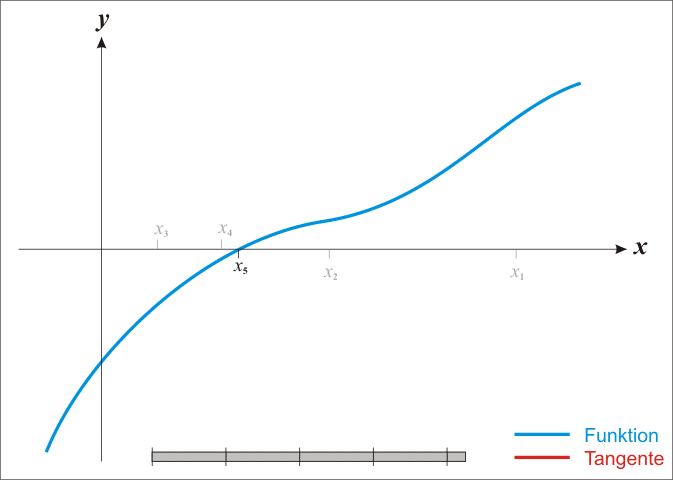
Метод Ньютона является очень мощным методом поиска корней функции, так как имеет квадратичную скорость сходимости - количество значащих цифр примерно удваивается с каждым шагом итерации, однако существуют и ограничения, затрудняющие его применение. Так, например, если начальное приближение недостаточно близко к решению, то метод может не сойтись, если производная не непрерывна в точке корня, то метод может расходиться в любой окрестности корня, если не существует вторая производная в точке корня, то скорость сходимости метода может быть заметно снижена, если производная в точке корня равна нулю, то скорость сходимости не будет квадратичной, а сам метод может преждевременно прекратить поиск, и дать неверное для заданной точности приближение.
Теорема Канторовича дает следующие условия применимости метода для поиска корней функции:
- функция должна быть ограничена;
- функция должна быть гладкой, дважды дифференцируемой;
- её первая производная f'(x) равномерно отделена от нуля;
- её вторая производная f''(x) должна быть равномерно ограничена.
Комментарии