Онлайн калькулятор: Калькулятор векторного произведения

Этот калькулятор ниже вычисляет векторное произведение двух векторов в трехмерном пространстве и отображает результат. На графике, первый вектор показан зеленым, второй - голубым, а векторное произведение показано красным. Теория и формула находятся ниже под калькулятором.

Калькулятор векторного произведения

Вектор а

Вектор b

Точность вычисления

Знаков после запятой: 2

Векторное произведение

Определение

Векторное произведение это операция с двумя векторами в трехмерном пространстве $\left(\mathbb {R} ^{3}\right)$ и обозначается она символом $\times$ . По двум заданным линейно независимым векторам $\mathbf {a}$ и $\mathbf {b}$ , векторное произведение, $\mathbf {a} \times \mathbf {b}$ , это вектор, который перпендикулярен обоим, $\mathbf {a}$ и $\mathbf {b}$ , и, таким образом, является нормалью к плоскости.

Векторное произведение определяется по формуле:

$\mathbf {a} \times \mathbf {b} =\left\|\mathbf {a} \right\|\left\|\mathbf {b} \right\|\sin(\theta )\ \mathbf {n}$ ,

где θ - это угол между a и b в плоскости, содержащей их (следовательно, это угол между 0° и 180°), ‖a‖ и ‖b‖ - это величины векторов a и b, и n - это единичный вектор, перпендикулярный плоскости, содержащей a и b в направлении, заданном по правилу правой руки. Если векторы a и b параллельны (угол θ между ними равен либо 0°, либо 180°), по формуле выше, векторное произведение a и b - это нулевой вектор, 0.

Условно, направление вектора n задается по правилу правой руки: если правая ладонь расположена таким образом, чтобы получилось совпадение большого пальца с первым вектором-сомножителем (a), а указательного – со вторым (b),то отведённый в сторону средний палец совпадёт с направлением вектора произведения (n).

Использование этой формулы подразумевает, что векторное произведение антикоммутативное, т.е. , b × a = −(a × b). Если указательный палец сонаправлен с вектором b, и и средний палец сонаправлен с вектором a, то большой палец будет указывать противоположное направление, сохраняя знак векторного произведения.

Следует обращать внимание на направленность системы координат, используя векторное произведение. Правило правой руки используется для правосторонней системы координат. В левосторонней координатной системе, направление вектора n задано по правилу левой руки и указывает в противоположных направлениях.

Формула

Нам нужен достаточно практичный способ вычисления векторного произведения для двух векторов. Для стандартного базиса в трехмерном пространстве, образованного векторами

$i=(1,0,0),\quad j=(0,1,0),\quad k=(0,0,1)$ ,

Можем написать следующие равенства из определения векторного произведения.
$i \times j = k \\ j \times k = i \\ k \times i = j \\ j \times i = -k \\ k \times j = -i \\ i \times k = -j \\ i \times i = j \times j = k \times k = 0$

Так как каждый вектор можно определить как линейную комбинацию трех изначальных векторов, то вектора можно записать так
$a=(x_1,y_1,z_1),\quad b=(x_2,y_2,z_2)$
т.е
$a=x_1i + y_1j+z_1k,\quad b=x_2i+y_2j+z_2k$ .

Таким образом, векторное произведение a и b записывается как
$a \times b=(x_1i + y_1j+z_1k) \times (x_2i+y_2j+z_2k)$ .

Если мы раскроем скобки, то получим
$a \times b=x_1x_2(i \times i)+x_1y_2(i \times j)+x_1z_2(i \times k)+y_1x_2(j \times i)+y_1y_2(j \times j)+y_1z_2(j \times k)+z_1x_2(k \times i)+z_1y_2(k \times j)+z_1z_2(k \times k)$

Формула может быть упрощена, при использовании базисных векторов, перечисленных выше
$a \times b=(y_1z_2-z_1y_2)i+(z_1x_2-x_1z_2)j+(x_1y_2-y_1x_2)k$

Кстати, выражение выше может быть записано как детерминант
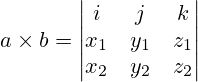
$a\times b ={\begin{vmatrix}i &j &k \\x_{1}&y_{1}&z_{1}\\x_{2}&y_{2}&z_{2}\\\end{vmatrix}}$

Последняя формула описывает результат векторного произведения с координатами.
$a \times b={\begin{pmatrix}y_1z_2-z_1y_2\\z_1x_2-x_1z_2\\x_1y_2-y_1x_2\end{pmatrix}}$

PLANETCALC Онлайн калькуляторы

Калькулятор векторного произведения

Эта страница существует благодаря следующим персонам

Timur

Mary Pichugina

Калькулятор векторного произведения

Вектор а

Вектор b

Векторное произведение

Определение

Формула

Похожие калькуляторы

Комментарии

PLANETCALC Онлайн калькуляторы

Калькулятор векторного произведения

Вектор а

Вектор b

Векторное произведение

Определение

Формула

Похожие калькуляторы

Комментарии

Поделиться этой страницей