Онлайн калькулятор: Объем части полусферы, отрезанной под углом

Калькулятор вычисляет объем части полусферы, полученной путем сечения полусферы плоскостью, проходящей на заданном расстоянии от центра полусферы под заданным углом.

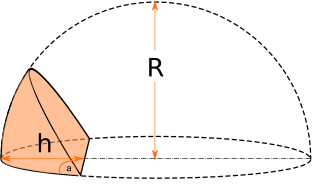
Угол может быть в пределах (0..180) градусов.Расстояние h не должно превышать диаметра полусферы. Формулы вычисления можно найти сразу под калькулятором.

Объем полусферы, рассеченной плоскостью под заданным углом

Радиус

Высота

Расстояние между центром основания полусферы и режущей плоскостью вдоль основания полусферы.

Угол

Угол в градусах между основанием полусферы и плоскостью разреза.

Точность вычисления

Знаков после запятой: 5

Объем

Формулы объема сечения полусферы плоскостью

Начинаем с простых случаев

Разрез проходит строго по центру полусферы, h=R

2)Центральный разрез полусферы, боковая проекция.

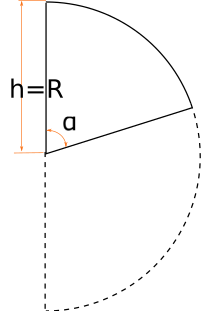
Это самый простой случай, формула получается путем легкой модификации формулы объема полусферы:
$V=\frac{2}{3}R^3\pi$
Следующим образом:
$V=\frac{2}{3}R^3\alpha$ , где a угол разреза в радианах.

Полусфера разрезана под углом 90 градусов

3)Прямой разрез полусферы. Боковая проекция.

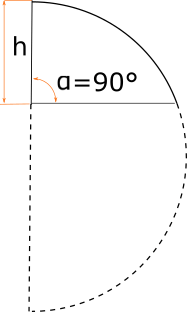
Если полусфера разрезана под прямым углом, мы попросту берем половину объема сечения сферы.

$V=\frac{\pi H^2(3R-H)}{6}$

Полусфера разрезана ниже центра h > R

4)Разрез ниже середины полусферы. Боковая проекция.

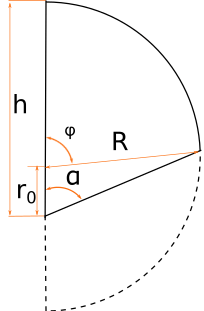
Если разрезать полусферу таким, образом, что центр полусферы окажется в части, для которой нужно вычислить объем мы получим самый сложный случай. Для такого случая мы вычисляем объем другой отрезанной части и вычитаем полученный объем из объема всей полусферы:
$V=\frac{2}{3}R^3\pi-V_d$
V_d вычисляется по формулам приведенным далее, с предварительным преобразованием угла $\alpha=\pi-\alpha$

Сечение проходит выше центра полусферы h < R

5) Разрез полусферы под углом выше центра

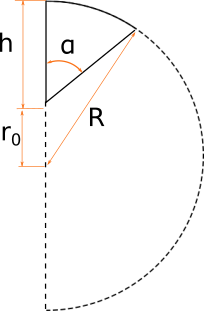
Это наиболее общий случай, который решается интегрированием по объему.
Разместим полусферу на координатной плоскости таким образом, чтобы секущая плоскость была параллельна плоскости Z-O-Y, центр полусферы в начале координат. Секущая плоскость будет удаена от плоскости Z-O-Y на расстояние sin(α)*r0, где r0=R-h расстояние от пересечения основания полусферы и секущей плоскости до центра полусферы:

6)Расположение разрезанной полусферы в системе координат

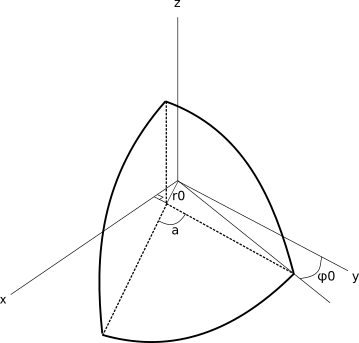
В линейной 3-мерной координатной системе секущая плоскость будет иметь уравнение $x=r_0 \sin \alpha$ .
В сферической системе координат (ISO): $r=\frac{r_0 \sin \alpha}{\sin \theta \cos \varphi}$ (1)
Далее будем решать интеграл в сферической системе координат:
$V=2\int_{\frac{\pi}{2}-\alpha}^{\frac{\pi}{2}-{\varphi}_0}d{\varphi}\int_{\theta_{\varphi}}^{\frac{\pi}{2}}\sin{\theta}d{\theta} \int_{r_{\varphi,\theta}}^R{r^2}d{r}$ (2)
Так как разрезанная полусфера расположена симметрично относительно плоскости X-O-Y мы будем интегрировать только половину возможного угла тета и домножим интеграл на 2.

Интервалы интегрирования

Интервал угла φ постоянный: $[\frac{\pi}{2}-\alpha-\frac{\pi}{2}-{\varphi}_0]$
Где a угол сечения к основанию полусферы в радианах
и согласно изображению (6) угол ${\varphi}_0=\arcsin(\frac{r_0 \sin \alpha}{R})$ (3)
Интервал радиусов
Верхняя граница упрается в радиус полусферы - R. Плоскость сечения ограничивает интервал снизу, согласно формуле (1) имеем:
$r_{\varphi,\theta}=\frac{r_0 \sin \alpha}{\sin \theta \cos \varphi}$ (4)
Интервалы угла θ
Так как мы интегрируем только верхнюю половину интервала θ то верхняя граница θ равна $\frac{\pi}{2}$ , а нижнюю можно выразить из формулы (1), принимая r=R. Таким образом:
$\theta_{\varphi}=\arcsin\left(\frac{r_0 \sin{\alpha}}{R\cos\varphi}\right)$ (5)
Используя (3) мы можем сократить формулу так:
$\theta_{\varphi}=\arcsin\left(\frac{\sin {\varphi}_{0}}{\cos\varphi}\right)$ (6)

Формула объема

Для получения формулы объема сечения полусферы, решим интеграл (2) в интервалах (3),(4),(6):

Интегрируем по r
$V=2\int_{\frac{\pi}{2}-\alpha}^{\frac{\pi}{2}-{\varphi}_0}d{\varphi}\int_{\theta_{\varphi}}^{\frac{\pi}{2}}\sin{\theta}d{\theta}\left.\frac{1}{3}r^3\right|_{\frac{r_0 \sin \alpha}{\sin \theta \cos \varphi}}^R$
Результат:
$V=\frac{2}{3}\int_{\frac{\pi}{2}-\alpha}^{\frac{\pi}{2}-{\varphi}_0}d{\varphi}\int_{\theta_{\varphi}}^{\frac{\pi}{2}}R^3\sin{\theta}-\frac{r_0^3 \sin^3 \alpha}{\cos^3 \varphi}d{\theta}$
Интегрируем по θ
$V=\frac{2}{3}\int_{\frac{\pi}{2}-\alpha}^{\frac{\pi}{2}-{\varphi}_0}d{\varphi}\left. \cot \theta \frac{r_0^3\sin^3 \alpha}{\cos^3 \varphi} - R^3 \cos\theta\right|_{\arcsin\left( \frac{\sin {\varphi}_{0}}{\cos \varphi}\right)}^{\frac{\pi}{2}}$
Результат:
$V=\frac{2}{3}\int_{\frac{\pi}{2}-\alpha}^{\frac{\pi}{2}-{\varphi}_0} R^2 r_0\sin\alpha \frac{\sqrt{\frac{\cos^2\varphi}{\sin^2{\varphi}_0}-1}}{\cos\varphi} - r_0^3\sin^3\alpha\frac{\sqrt{\frac{\cos^2\varphi}{\sin^2{\varphi}_0}-1}}{\cos^3\varphi} d{\varphi}$
Интегрируем по φ
$V=\frac{2}{3}R^2 r_0 \sin \alpha \left( \csc{\varphi}_0 \arcsin\frac{\sin\varphi}{\cos{\varphi}_0} - \arctan\frac{\sin\varphi \sin {\varphi}_0}{\sqrt{\cos^2\varphi-\sin^2\varphi_0}} \right)$
$- \frac{r_0^3\sin^3 \alpha}{3}\left( \cot^2{\varphi}_0 \arctan\frac{\sin\varphi \sin {\varphi}_0}{\sqrt{\cos^2\varphi-\sin^2\varphi_0}} +\csc {\varphi}_0 \tan\varphi \sec\varphi \sqrt{\cos^2\varphi-\sin^2\varphi_0} \right)\Bigg|_{\frac{\pi}{2}-\alpha}^{\frac{\pi}{2}-{\varphi}_0}$
Получаем окончательную формулу:
$V= \frac{r_0^3\sin^3 \alpha}{3}\left( \cot^2{\varphi}_{0}(K_2- \frac{\pi}{2}) +K_1\csc {\varphi}_0 \cot\alpha \csc\alpha\right)$
$-\frac{2}{3}R^2 r_0 \sin \alpha \left( \csc{\varphi}_0 \left(\arcsin\left[\frac{\cos\alpha}{\cos{\varphi}_0}\right]-\frac{\pi}{2}\right) - K_2+\frac{\pi}{2}\right)$
Где:
$K_1=\sqrt{\sin^2\alpha-\sin^2\varphi_0}$ ,
$K_2=\arctan\frac{\cos\alpha \sin {\varphi}_0}{K_1}$ .