Объем части полусферы, отрезанной под углом
Объем несимметрично отрезанной части полусферы.
Калькулятор вычисляет объем части полусферы, полученной путем сечения полусферы плоскостью, проходящей на заданном расстоянии от центра полусферы под заданным углом.
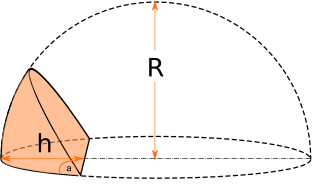
Угол может быть в пределах (0..180) градусов.Расстояние h не должно превышать диаметра полусферы. Формулы вычисления можно найти сразу под калькулятором.
Формулы объема сечения полусферы плоскостью
Начинаем с простых случаев
Разрез проходит строго по центру полусферы, h=R
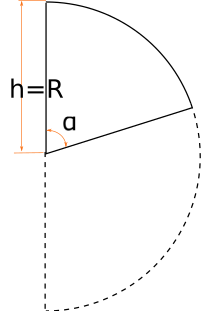
Это самый простой случай, формула получается путем легкой модификации формулы объема полусферы:
Следующим образом:
, где a угол разреза в радианах.
Полусфера разрезана под углом 90 градусов
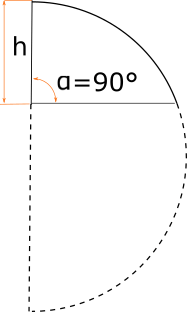
Если полусфера разрезана под прямым углом, мы попросту берем половину объема сечения сферы.
Полусфера разрезана ниже центра h > R
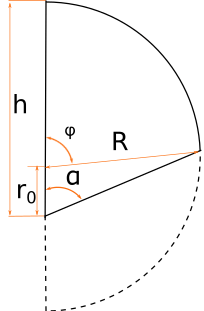
Если разрезать полусферу таким, образом, что центр полусферы окажется в части, для которой нужно вычислить объем мы получим самый сложный случай. Для такого случая мы вычисляем объем другой отрезанной части и вычитаем полученный объем из объема всей полусферы:
Vd вычисляется по формулам приведенным далее, с предварительным преобразованием угла
Сечение проходит выше центра полусферы h < R
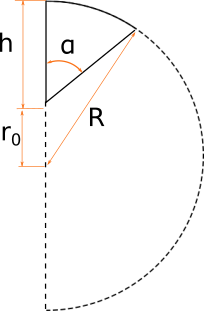
Это наиболее общий случай, который решается интегрированием по объему.
Разместим полусферу на координатной плоскости таким образом, чтобы секущая плоскость была параллельна плоскости Z-O-Y, центр полусферы в начале координат. Секущая плоскость будет удаена от плоскости Z-O-Y на расстояние sin(α)*r0, где r0=R-h расстояние от пересечения основания полусферы и секущей плоскости до центра полусферы:
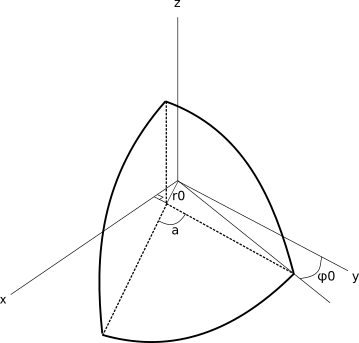
В линейной 3-мерной координатной системе секущая плоскость будет иметь уравнение .
В сферической системе координат (ISO): (1)
Далее будем решать интеграл в сферической системе координат:
(2)
Так как разрезанная полусфера расположена симметрично относительно плоскости X-O-Y мы будем интегрировать только половину возможного угла тета и домножим интеграл на 2.
Интервалы интегрирования
- Интервал угла φ постоянный:
Где a угол сечения к основанию полусферы в радианах
и согласно изображению (6) угол(3)
- Интервал радиусов
Верхняя граница упрается в радиус полусферы - R. Плоскость сечения ограничивает интервал снизу, согласно формуле (1) имеем:
(4)
- Интервалы угла θ
Так как мы интегрируем только верхнюю половину интервала θ то верхняя граница θ равна, а нижнюю можно выразить из формулы (1), принимая r=R. Таким образом:
(5)
Используя (3) мы можем сократить формулу так:
(6)
Формула объема
Для получения формулы объема сечения полусферы, решим интеграл (2) в интервалах (3),(4),(6):
-
Интегрируем по r
Результат:
-
Интегрируем по θ
Результат:
- Интегрируем по φ
Получаем окончательную формулу:
Где:
,
.
Комментарии