Инволюта угла
Вычисление инволюты угла и нахождение угла по заданной инволюте.
Этот материал распространяется на условиях лицензии Creative Commons Attribution/Share-Alike License 3.0 (Unported). Это означает, что вы можете размещать этот контент на своем сайте или создавать на его основе собственный (в том числе и в коммерческих целях), при условии сохранения оригинального лицензионного соглашения. Кроме того, Вы должны отметить автора этой работы, путем размещения HTML ссылки на оригинал работы https://planetcalc.ru/993/. Пожалуйста оставьте без изменения все ссылки на других авторов данной работы или работы, на основе которой создана данная работа (если таковые имеются в спроводительном тексте).
Поступила вот просьба сделать калькулятор для расчета цилиндрических шестерён — Техника,машиностроение.
Погружаясь в тему шестерён и их расчетов, встретил понятие инволюта, а потом — эвольвента. Показалось занятным и заслуживающим отдельных калькуляторов. Калькуляторы смотри ниже — первый рассчитывает инволюту, два следующих по заданной инволюте находят угол. Интересующимся — текст про инволюту после калькуляторов.
Так вот, в дифференциальной геометрии кривых эвольвента — это кривая, нормаль в каждой точке которой является касательной к исходной кривой (см. Эвольвента в Википедии).
Поскольку сразу осознать сказанное выше сложно, перескажу своими словами более образное определение, данное в английской версии статьи (см. Involute on Wikipedia).
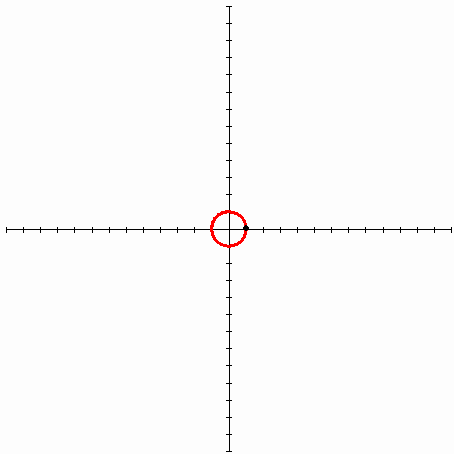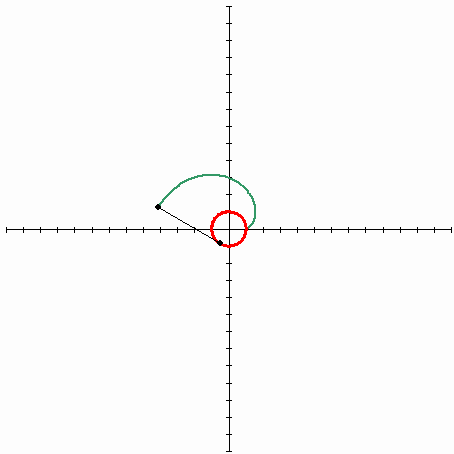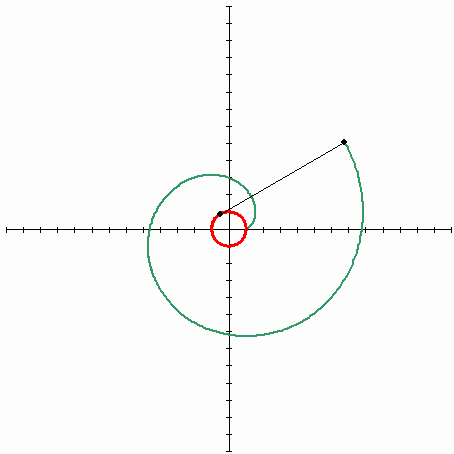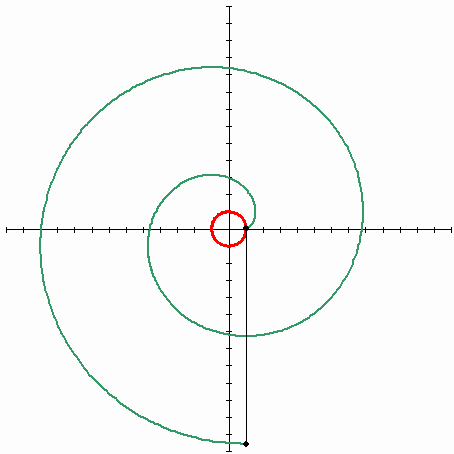
Итак, представим себе катушку ниток, где свободный край нити лежит на катушке. Если взять этот край и начать разматывать нить, все время держа ее натянутой, край нити опишет некую кривую, которая и будет эвольвентой, причем эвольвентой окружности (катушка суть исходная кривая, представляющая собой окружность).
Рисунок ниже изображает эвольвенту окружности (Источник — Википедия). Красная линия — исходная кривая (окружность), черная — натянутая нить, зеленая — траектория конца нити, кривая, называемая эвольвентой окружности.
Что касается инволюты — в англоязычных источниках, как я понял, термин инволюта (involute) применяется взаимозаменяемо с термином эвольвента (evolvent). То есть может обозначать как саму кривую, так и ее функцию. В русскоязычных источниках, которые я видел, эвольвента - это кривая, а инволюта - ее функция.
Думаю, что такое эвольвента, стало более менее ясно после картинки сверху. Теперь разберемся, что это за функция такая.
В этом нам поможет рисунок, который я нарисовал
На рисунке отрезок равен дуге
(потому что эта наша «нить»). Угол «фи», соответствующий дуге
называется углом развернутости эвольвенты, и состоит суммы угла «тета» (эвольвентного угла) и угла «альфа» (угла давления). Длина дуги
Поскольку — прямоугольный треугольник, то
Приравнивая эти две дуги друг к другу, получим , откуда
Вот эта-то функция — и называется инволютой, или эвольвентной функцией.
Уравнения эвольвентной кривой в полярных координатах выглядят так
По построению видно, что угол «альфа» может меняться от 0 до 90, не включая 90, так как в таком случае прямая KK будет параллельна MxN.
Зачем это все? Эвольвента окружности используется в эвольвентном зацеплении — зубчатом зацеплении, в котором профили зубьев очерчены по эвольвенте окружности. При эвольвентном зацеплении общая нормаль к соприкасающимся профилям зубьев всегда совпадает с общей касательной к основным окружностям. Эта касательная называется линией зацепления, так как по ней перемещается точка касания зубьев при движении колёс (картинка). Это наиболее распространенный вид зубчатого зацепления.
А инволюта используется в расчетах, связанных с эвольвентным зацеплением. Причем возникает задача как расчета самой инволюты (что просто), так и обратная задача — нахождение угла давления по его инволюте. Вот обратная задача является не такой простой, ибо уравнение является трансцендентным уравнением, и решить его можно только численными методами.
В завершение рассмотрим численные методы, использованные в калькуляторах выше — метод Ласкина и метод Ченга (подробнее — здесь)
Метод Ласкина (Laskin)
Основан на методе Ньютона, заключающемся в итерационной процедуре вычисления
Ноу-хау, как я понимаю, здесь в выборе начального значения, которое по методу Ласкина вычисляется как
, где I — заданное значение инволюты.
Для вычисления следующих приближений после раскрытия производной получается выражение
В калькуляторе используется пять итераций, но уже четыре должны давать точность до шести знаков после запятой. Метод работает для значений инволюты в диапазоне от 0 до 1, то есть можно находить углы от 0 до 64.87 градусов. На практике этого хватает. Для нахождения инволюты выпускаются таблицы, подобные таблицам тригонометрических функций, так вот там приводимый диапазон углов от 0 до 60.
Метод Ченга (Cheng)
Основан на нахождении приближенного значения с помощью асимптотических кривых. Ченг вывел следующую формулу:
Метод работает для значения инволюты строго меньших 1.8, то есть может находить углы примерно до 71.87 градуса. А дальше оно и не надо — при приближении к 90 тангенс стремится к бесконечности, со всеми вытекающими отсюда последствиями, и, в общем, ну не бывает зубчатых передач с такими большими углами.
Комментарии