Сегмент шара
Вычисление площади поверхности и объема шарового сегмента или шарового слоя.

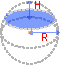
Шаровым сегментом называется часть шара, отсеченная от него плоскостью.
Формулы:
— площадь боковой поверхности
— площадь основания
— формула объема

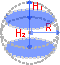
Шаровой слой — часть шара, ограниченная двумя параллельными плоскостями, пересекающими шар.
Формулы:
— площадь боковой поверхности
— объем
Ссылка скопирована в буфер обмена
Похожие калькуляторы
Геометрия Инженерные объем площадь боковой поверхности площадь поверхности полусфера сферический сегмент сферический слой шаровой сегмент шаровой слой
PLANETCALC, Сегмент шара
Комментарии