Поверхностное натяжение. Масса и объем капли
Этот калькулятор рассчитывает массу и объем капли при отрыве от капиллярной трубки.
Эта страница существует благодаря следующим персонам
 | Timur
|
Этот материал распространяется на условиях лицензии Creative Commons Attribution/Share-Alike License 3.0 (Unported). Это означает, что вы можете размещать этот контент на своем сайте или создавать на его основе собственный (в том числе и в коммерческих целях), при условии сохранения оригинального лицензионного соглашения. Кроме того, Вы должны отметить автора этой работы, путем размещения HTML ссылки на оригинал работы https://planetcalc.ru/2296/. Пожалуйста оставьте без изменения все ссылки на других авторов данной работы или работы, на основе которой создана данная работа (если таковые имеются в спроводительном тексте).
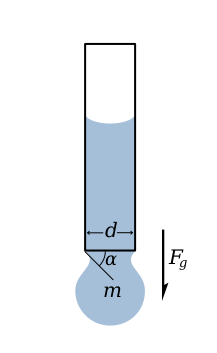
На представленной здесь картинке, капля задерживается на конце трубки за счет силы поверхностного натяжения. Сила эта пропорциональна длине границы между жидкостью и трубкой и равна
,
где — коэффициент поверхностного натяжения, измеряемый в ньютонах на метр, Н/м.
Капля не отрывается, очевидно, пока эта сила способна нейтрализовать силу тяжести, действующую на каплю в вертикальной проекции, то есть
При увеличении массы капли, то есть при ее росте, угол альфа будет стремиться к 90 градусам, и, в состоянии равновесия сил, формула примет вид
, откуда
масса капли
Рассчитав подобным образом массу и зная плотность жидкости, объем посчитать тривиально.
На самом деле, конечно, не вполне так, потому что место отрыва обычно немного ниже конца трубки, и отрыв происходит в месте формирования так называемой шейки, где диаметр несколько меньше чем диаметр трубки, но там, где не требуется очень большая точность, этим обычно пренебрегают.
Мне захотелось также оценить максимальный диаметр трубки, при котором еще возможно образование на ее конце капель. В оценке я исходил из того, что образование капли возможно тогда, когда силы поверхностного натяжения еще способны удерживать как минимум полусферу. Отсюда, опять же зная плотность жидкости, можно представить формулу следующим образом
и, соответственно,
Пара слов о калькуляторе ниже. Во первых, калькулятор не рассчитывает массу и объем капли при превышении диаметра трубки оценки, сделанной выше. Во-вторых, значения плотности и коэффициента поверхностного натяжения по умолчанию соответствуют воде.
Комментарии