Онлайн калькулятор: Конус

Конус - трехмерная фигура, имеющая одно основание и одну вершину.

Косой конус - конус у которого вершина не находится по центру основания.
Правильный конус имеет вершину четко выровненную по центру основания. Основание правильного конуса не обязательно должно быть кругом.

Объем конуса: $V=\frac{1}{3}S_bH$ , где _ $S_b$ _ площадь основания конуса, $H$ -кратчайшее расстояние от вершины конуса до основания.

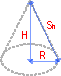
Если основание правильного конуса - круг, то такой конус будет правильным круговым конусом.
Такой конус характеризуется радиусом основания и высотой- расстоянием от вершины до центра основания. Объем правильного кругового конуса: $V=1/3\pi R^2H$

Площадь поверхности конуса выражается следующей формулой: $S=S_{base} + S_{lateral}=\pi R^2 + \pi R H_s=\pi R^2 + \pi R \sqrt{R^2+H^2}$ , где $H_s= \sqrt{R^2+H^2}$ - наклонная высота конуса, измеряемая как расстояние от вершины конуса до любой точки на периметре основания.

Конус

Радиус (R)

Высота (H)

Точность вычисления

Знаков после запятой: 5

Объем

Площадь боковой поверхности

Площадь поверхности

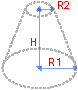
Объем правильного кругового усеченного конуса $V=\frac{1}{3}\pi (R_1^2+R_1 R_2 + R_2 ^2)H$
Площадь поверхности правильного усеченного конуса $S=\pi R_1^2 + \pi R_2^2 + \pi (R_1+R_2)\sqrt{(R_1-R_2)^2 + H^2}$

Усеченный конус

Радиус 1 (R1)

Радиус 2 (R2)

Высота (H)

Точность вычисления

Знаков после запятой: 5

Объем

Площадь боковой поверхности

Площадь поверхности

PLANETCALC Онлайн калькуляторы

Конус

Эта страница существует благодаря следующим персонам

Anton

Конус

Усеченный конус

Похожие калькуляторы

Комментарии

PLANETCALC Онлайн калькуляторы

Конус

Усеченный конус

Похожие калькуляторы

Комментарии

Поделиться этой страницей