Расчет спирали
Расчет неизвестных размеров спирали по известным размерам. Параметры спирали: внешний диаметр, внутренний диаметр, толщина (шаг спирали), длина спирали, число витков.
Данный калькулятор позволяет рассчитать неизвестные параметры спирали по известным параметрам.

Есть пять параметров спирали: внешний диаметр - D, внутренний диаметр - d, толщина (шаг спирали) - t, длина спирали - L, число витков - n. Есть уравнения, устанавливающие связь между этими параметрами (формулы приведены под калькулятором). По этим уравнениям, зная какие-либо три параметра, можно вычислить два оставшихся неизвестных параметра.
Где мы встречаемся со спиралью? Чаще всего при покупке каких-либо материалов в рулонах, будь то рулоны обоев или рулоны туалетной бумаги. Используя калькулятор ниже, можно рассчитать, например, количество погонных метров в рулоне т.е. длину спирали, зная или измерив толщину материала или посчитав количество витков, и измерив внутренний и внешний диаметры рулона. Калькулятор также может решать и обратные задачи , например, по длине спирали и её диаметрам найти толщину и количество витков спирали. Теория и формулы, как обычно, приведены под калькулятором.
При вводе известных параметров проверяйте правильно ли указана размерность для введенных значений. 20 метров это не тоже самое что 20 миллиметров...
Архимедова спираль
Под Архимедовой спиралью понимают плоскую кривую (спираль), которая отображает траекторию точки М, равномерно движущейся вдоль луча ОА, в то время как сам луч равномерно вращается вокруг точки О.

Если обозначить расстояние от О до М как ρ, а угол поворота луча как φ, то в полярных координатах зависимость расстояния вдоль луча от угла поворота луча можно записать как
,
где k это параметр спирали, соответствующий величине смещения точки вдоль луча при повороте на один радиан. Повороту на 2π будет соответствовать смещение на 2πk.
Так как 2π это полный оборот, число a, также называемое шагом спирали, будет соответствовать расстоянию между двумя соседними витками спирали и начальное уравнение можно переписать в виде.
Так как шаг спирали постоянный, то чем дальше от центра, тем больше витки спирали по форме напоминают окружность. К слову, если движение точки описывается другим уравнением, то это какая-то другая спираль.
Для того, чтобы вывести формулу вычисления длины спирали, рассмотрим бесконечно малое приращение длины.
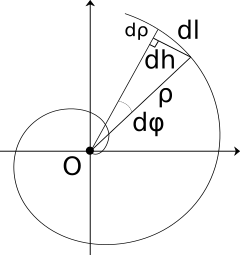
Бесконечно малый отрезок дуги dl можно представить как гипотенузу прямоугольного треугольника с катетами dρ и dh. По теореме Пифагора гипотенуза равна
Бесконечно малый отрезок dh можно заменить на бесконечно малую часть дуги окружности с радиусом ρ, длина которой ρdφ.
Из уравнения спирали заменяем ρ на kφ, и dρ на kdφ
Таким образом мы получили зависимость dl от dφ. Чтобы найти длину L достаточно взять интеграл от начального угла поворота луча до конечного угла поворота луча.
Интеграл я выводить не буду, его уже вывели до меня. Конечный результат
В случае если спираль выходит из точки О, то есть начальный угол поворота луча равен 0, формула упрощается
Если мы говорим о рулоне, то там скорее всего начальный угол все же не равен нулю, то есть есть ненулевой внутренний диаметр (например, там есть втулка). Как же перейти от углов к диаметрам, и найти число витков спирали?
Число витков спирали связано с углами следующим очевидным соотношением:
Диаметры можно связать с углом непосредственно по уравнению спирали (если вспомнить что диаметр это два радиуса)
Эти соотношения и используются для нахождения неизвестных параметров спирали по известным. Осталось только заметить, что уравнение длины является трансцендентным, и решение обратной задачи - по известной длине найти что-то неизвестное, невозможно найти аналитически. Для получения решения приходится прибегать к численным методам, в частности, в калькуляторе выше используется метод секущих.
Комментарии