PLANETCALC Онлайн калькуляторы

Войти
УчебаМатематикаГеометрия

Системы координат в пространстве

Преобразование координат из / в декартову, цилиндрическую и сферическую систему координат.

Эта страница существует благодаря следующим персонам

A

Anton

Timur

Timur

Создан: 2018-10-20 16:02:27, Последнее изменение: 2024-04-10 08:43:50
Creative Commons Attribution/Share-Alike License 3.0 (Unported)

Этот материал распространяется на условиях лицензии Creative Commons Attribution/Share-Alike License 3.0 (Unported). Это означает, что вы можете размещать этот контент на своем сайте или создавать на его основе собственный (в том числе и в коммерческих целях), при условии сохранения оригинального лицензионного соглашения. Кроме того, Вы должны отметить автора этой работы, путем размещения HTML ссылки на оригинал работы https://planetcalc.ru/7952/. Пожалуйста оставьте без изменения все ссылки на других авторов данной работы или работы, на основе которой создана данная работа (если таковые имеются в спроводительном тексте).

Этот калькулятор предназначен для преобразования координат в пространстве, заданных в трех системах:

  • Прямоугольной (декартовой)
  • Цилиндрической
  • Сферической
    Прямоугольная, цилиндрическая и сферическая системы координат
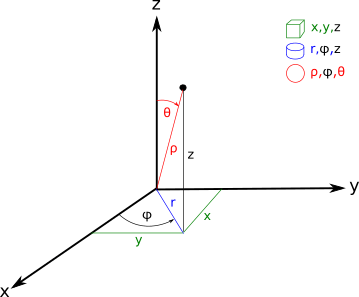
    Прямоугольная, цилиндрическая и сферическая системы координат

Прямоугольная система координат

Определяет точку в пространстве при помощи трех чисел : x, y, z. Каждое число соответствует длине кратчайшего отрезка, проложенного параллельно одноименной оси координат до плоскости, образованной другими осями координат. Длина берется со знаком минус, если точка находится со стороны отрицательных значений шкалы координат.

Цилиндрическая система координат

Определяет точку в пространстве при помощи радиуса r, угла азимута φ, и высоты z. Высота z соответствует координате z в прямоугольной системе координат. Радиус r - всегда неотрицательное число, задающее минимальное расстояние от точки в пространстве до оси z. Азимутальный угол φ - значение в диапазоне 0 ..360 градусов - определяет угол, между положительной полуосью x и радиусом, проложенным через проекцию точки на плоскость, образованную осями x и y.

Сферическая система координат

Определяет точку в пространстве при помощи радиуса ρ, азимута φ, и полярного угла θ. Азимут φ совпадает со значением азимута в цилиндрических координатах. Радиус ρ - расстояние от центра координат, до точки. Полярный угол образован положительной полуосью z и радиусом из центра координат до точки в пространстве.

PLANETCALC, Прямоугольные координаты в пространстве

Прямоугольные координаты в пространстве

Знаков после запятой: 2

Цилиндрические координаты

Радиус (r)
 
Азимут (φ), градусы
 
Высота (z)
 

Сферические координаты

Радиус (ρ)
 
Азимут (φ), градусы
 
Полярный угол (θ), градусы
 

Формулы преобразования декартовых координат

Радиус в цилиндрической системе:
r = \sqrt{x^2+y^2}
Радиус в сферической системе:
\rho = \sqrt{x^2+y^2+z^2}
Азимут:
\varphi=Arctan(y,x), см Арктангенс с двумя аргументами

Полярный угол:
\theta=\arctan\frac{\sqrt{x^2+y^2}}{z}

PLANETCALC, Цилиндрические координаты

Цилиндрические координаты

Знаков после запятой: 2

Прямоугольные координаты

x
 
y
 
z
 

Сферические координаты

Радиус (ρ)
 
Азимут (φ), градусы
 
Полярный угол (θ), градусы
 

Формулы преобразования цилиндрических координат

Декартовы координаты:
x=r\cos\varphi,
y=r\sin\varphi

Радиус в сферической системе:
\rho = \sqrt{r^2+z^2}
Полярный угол:
\theta=Arctan(z,r), см Арктангенс с двумя аргументами

PLANETCALC, Сферические координаты

Сферические координаты

Знаков после запятой: 2

Прямоугольные координаты

x
 
y
 
z
 

Цилиндрические координаты

Радиус (r)
 
Азимут (φ), градусы
 
Высота (z)
 

Формулы преобразования сферических координат

Декартовы координаты:
x=\rho\sin\theta\cos\varphi,
y=\rho\sin\theta\sin\varphi,
z=\rho\cos\theta

Радиус в цилиндрической системе:
r = \rho\sin\theta

Ссылка скопирована в буфер обмена

Похожие калькуляторы

 #геометрия #координаты 3d Геометрия декартовы координаты конверторы координаты Математика система координат Системы координат сферические координаты цилиндрические координаты
PLANETCALC, Системы координат в пространстве
Anton2024-04-10 08:43:50

Комментарии