Развертка (выкройка) сферы
Развертка сферы на плоскость. Калькулятор вычисляет основные параметры развертки, а также выводит координаты точек для построения развертки одной доли.
Этот материал распространяется на условиях лицензии Creative Commons Attribution/Share-Alike License 3.0 (Unported). Это означает, что вы можете размещать этот контент на своем сайте или создавать на его основе собственный (в том числе и в коммерческих целях), при условии сохранения оригинального лицензионного соглашения. Кроме того, Вы должны отметить автора этой работы, путем размещения HTML ссылки на оригинал работы https://planetcalc.ru/6066/. Пожалуйста оставьте без изменения все ссылки на других авторов данной работы или работы, на основе которой создана данная работа (если таковые имеются в спроводительном тексте).
Калькулятор рассчитывает параметры развертки сферы на плоскости. Картинка ниже иллюстрирует задачу.
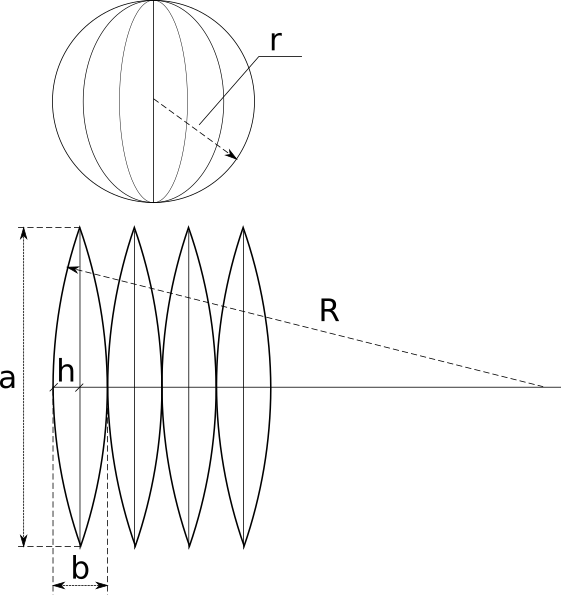
Итак, нам известен радиус сферы r и число долей на которое мы хотим ее разбить n. Для описания развертки нам надо найти высоту «дольки» a, ширину «дольки» b, и радиус R большой дуги, на которой построена «долька». Формулы расчета и объяснения, как обычно, приведены под калькулятором.
С высотой все понятно — это половина длины окружности, которую можно получить при сечении сферы плоскостью, проходящей через центр. Таким образом,
.
С шириной тоже все понятно — это часть той же окружности, полученная при разбиении всей окружности на n частей:
Радиус дуги можно вычислить по длине хорды (это а) и высоте сегмента (это h=b/2) по следующей формуле (см. Сегмент круга).
В принципе, найдя a и b, считать радиус R даже не обязательно — его можно найти по построению, что иллюстрирует следующая картинка.
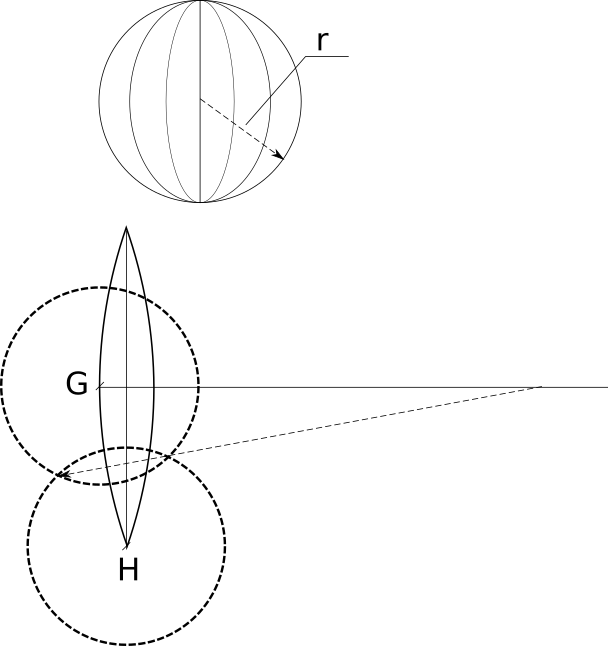
Для нахождения радиуса из точек G и H надо провести две окружности, так, чтобы они пересекались — прямая, проведенная через точки пересечения, пересечет среднюю линию в точке центра окружности, на дуге которой лежат G и H.
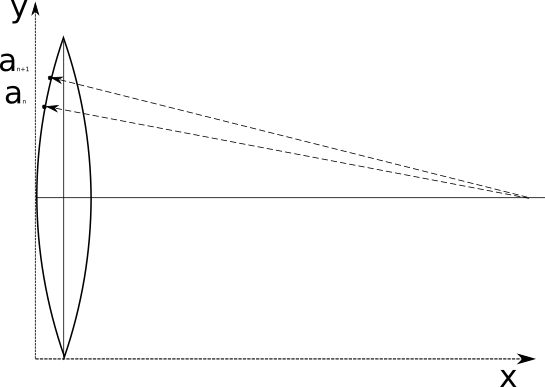
Несмотря на всю простоту, у метода есть один недостаток — а именно, ему нужно очень много места сбоку для радиуса, и чем больше число долек, на которое мы хотим разбить сферу, тем больше радиус большой дуги. Не везде будет возможность найти столько места и такой большой «циркуль», чтобы нарисовать дугу. Поэтому калькулятор, кроме расчета параметров «дольки», также рассчитывает координаты точек, лежащих на дуге — можно строить дуги дольки по точкам, не используя радиус. Для того, чтобы рассчитать координаты точек, надо пометить флажок «Сгенерировать точки развертки», и указать число точек — дуга будет разбита на заданное число точек с равным угловым шагом, как показано на рисунке:
Комментарии