Определение параметров правильного многоугольника по радиусам вписанной и описанной окружности
Определение числа сторон и длины одной стороны правильного многоугольника, если задан радиус описанной и радиус вписанной окружности.
Этот материал распространяется на условиях лицензии Creative Commons Attribution/Share-Alike License 3.0 (Unported). Это означает, что вы можете размещать этот контент на своем сайте или создавать на его основе собственный (в том числе и в коммерческих целях), при условии сохранения оригинального лицензионного соглашения. Кроме того, Вы должны отметить автора этой работы, путем размещения HTML ссылки на оригинал работы https://planetcalc.ru/2823/. Пожалуйста оставьте без изменения все ссылки на других авторов данной работы или работы, на основе которой создана данная работа (если таковые имеются в спроводительном тексте).
Вновь приходится возвращаться к теме описанной и вписанной окружности и правильному многоугольнику. Казалось бы, эта тема была закрыта калькуляторами Длина стороны правильного многоугольника для определения длины стороны многоугольника по радиусу и числу сторон и Правильный многоугольник. Описанная и вписанная окружность для определения радиуса по длине стороны и числу сторон, но нет.
Посетитель сайта попросил буквально следующее: «Сделайте пожалуйста такой калькулятор, который зная радиус вписанной и описанной окружностей найдет длину стороны многоугольника».
То есть, задача формулируется так: некоторый правильный многоугольник вписан в окружность с известным радиусом и вокруг него описана окружность с другим известным радиусом. Требуется найти параметры этого правильного многоугольника: число сторон и длину одной стороны.
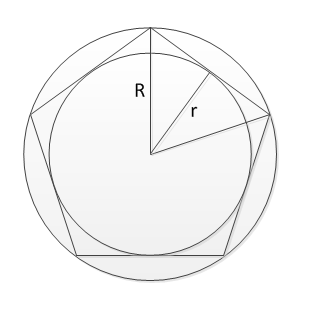
Чтобы было понятнее, графически эта ситуация изображена на картинке слева.
Посмотрев внимательно на треугольник, образованный перпендикуляром из центра окружности к стороне многоугольника (радиус вписанной окружности r), отрезком, соединяющим центр окружности и ближайшую к перпендикуляру вершину многоугольника (радиус описанной окружности R), и собственно, половиной стороны многоугольника, нетрудно заметить, что радиусы связаны между собой соотношением
где угол альфа, опирающийся на вершины многоугольника, связан следующим соотношением с числом сторон многоугольника n:
Таким образом, известные радиусы описанной и вписанной окружности дают нам однозначное соответствие с числом сторон правильного многоугольника.
Длина стороны определяется тривиально.
Теперь по поводу калькулятора — поскольку в расчете есть иррациональное число, получить по этой формуле целое число сторон невозможно. Но, с другой стороны, мы-то знаем, что число сторон — это целое число. Поэтому калькулятор сначала вычисляет число сторон как есть, потом округляет до ближайшего целого, и, исходя из этого целого числа, делает расчет длины стороны и обратный расчет одного из радиусов (из чистого любопытства).
Комментарии