Объем эллиптического параболоида
Этот онлайн калькулятор вычисляет объем эллиптического параболоида по высоте и длине полуосей (или радиусу в случае параболоида вращения).
Эта страница существует благодаря следующим персонам
 | Timur
|
Этот материал распространяется на условиях лицензии Creative Commons Attribution/Share-Alike License 3.0 (Unported). Это означает, что вы можете размещать этот контент на своем сайте или создавать на его основе собственный (в том числе и в коммерческих целях), при условии сохранения оригинального лицензионного соглашения. Кроме того, Вы должны отметить автора этой работы, путем размещения HTML ссылки на оригинал работы https://planetcalc.ru/9947/. Пожалуйста оставьте без изменения все ссылки на других авторов данной работы или работы, на основе которой создана данная работа (если таковые имеются в спроводительном тексте).
Формула для расчета приведена под калькулятором.
Объем эллиптического параболоида
Формула объема эллиптического параболоида
Если взять параболу, и начать вращать ее вокруг своей оси в трехмерном пространстве, мы получим поверхность вращения, называемую параболоидом вращения. Сечение параболоида вращения плоскостью c уравнением z = h (h＞0) (параллельной осям X и Y) будет образовывать окружность. Если параболоид вращения равномерно сжать/растянуть, то в сечение плоскостью будет образовывать эллипс, а сам параболоид будет называться эллиптическим параболоидом.
Объём эллиптического параболоида — это объём фигуры образованной параболоидом и плоскостью, перпендикулярной оси симметрии параболоида. Правильнее конечно говорить об объеме сегмента эллиптического параболоида. Такая фигура будет характеризоваться высотой H, а также длинами полуосей эллипса, образованного сечением, a и b (см. рисунок).
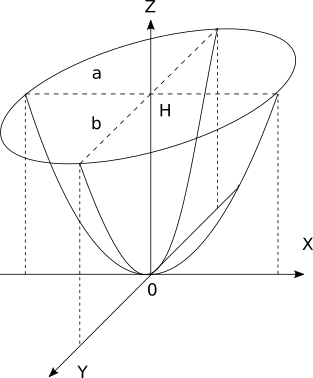
Формула объема такой фигуры
В случае параболоида вращения, a = b = r и формула равна
По формуле выше можно заметить, что объем сегмента параболоида составляет половину объема цилиндра с тем же основанием и той же высотой. Этот результат был получен еще Архимедом.
Комментарии