Подсчет труб с торца
Подход к подсчету числа вложенных окружностей меньшего радиуса при известной длине описывающей окружности большего радиуса. Создано по запросу пользователя.
Этот материал распространяется на условиях лицензии Creative Commons Attribution/Share-Alike License 3.0 (Unported). Это означает, что вы можете размещать этот контент на своем сайте или создавать на его основе собственный (в том числе и в коммерческих целях), при условии сохранения оригинального лицензионного соглашения. Кроме того, Вы должны отметить автора этой работы, путем размещения HTML ссылки на оригинал работы https://planetcalc.ru/957/. Пожалуйста оставьте без изменения все ссылки на других авторов данной работы или работы, на основе которой создана данная работа (если таковые имеются в спроводительном тексте).
Собственно, идем по следам запроса подсчет труб с торца.
Если вкратце — имеется пучок труб, чем-то связанных. Длину «веревки» можно померить. Радиус одной трубы — тоже. Требуется определить число труб в пучке без утомительного пересчитывания — расчетом.
Здравый смысл, впрочем, подсказывает, что расчетом совсем точно число труб в пучке определить нельзя — слишком много факторов. Окружность может быть неправильной, например, трубы могут улечься неравномерно и т. д.
Так что совсем без пересчитывания не получится, но задача сама по себе интересная, и можно попытаться вывести оценку сверху. Ну то есть рассчитать число труб для некоего идеального случая, тогда в реальности в пучке будет не больше труб, чем было рассчитано.
Калькулятор, который делает оценку сверху ниже, а рассуждения, которые привели к выводу этой оценки, как водится, под ним — для любознательных.
Идеальный случай — все трубы лежат ровно, правильная окружность и т. п. В общем, некоторые упрощения задачи, позволяющие применить геометрические знания и математический расчет :)
Кстати, оценку сверху тоже можно получать несколькими способами, и, в общем, они будут справедливы. Тут ведь главное как можно ближе приблизиться к реальному числу.
Например, вот самая простая оценка сверху:
-
По длине описывающей окружности находим ее площадь, или площадь сечения всего пучка:
-
По радиусу трубы находим ее площадь сечения:
- Делим общую площадь сечения на площадь сечения одной трубы.
Очевидно, что это будет оценка сверху — больше труб, чем получится в результате, в данную окружность не впихнешь. Но эта оценка сверху будет не очень точной, так как очевидно, что трубы лежат не вплотную друг к другу, а с зазорами, и часть общей площади сечения расходуется на дырки между трубами. См. картинку
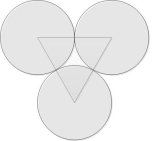
Надо учесть эти потери и сделать оценку числа труб более точной. Для начала разберемся с площадью зазора между трубами. Для этого рассмотрим треугольник, вершины которого образованы центрами соприкасающихся окружностей. Каждая сторона, очевидно, равна двум радиусам, и по формуле Герона его площадь равна . Площадь эта состоит из полезного пространства, занятого тремя секторами (от каждой окружности), и дырки. Сектора эти, очевидно, имеют угол в 180 градусов, а значит площадь всех трех секторов равна половине площади окружности
.
Таким образом, отношение полезной площади к общей площади треугольника равно
Самое замечательное в этом выводе то, что это соотношение никоим образом не зависит от радиуса.
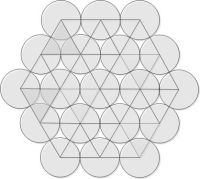
Идем дальше. Как видно из рисунка, «неплотно» упакованные окружности можно представить в виде «плотно» упакованных треугольников с дыркой посередине. Таким образом, имея общую площадь всего пучка, и считая, что это пучок треугольников — из соотношения выведенного выше, можно найти, сколько полезной площади в данном пучке — после чего разделить полученную полезную площадь на площадь одной окружности, получив, таким образом, еще одну оценку сверху числа труб в пучке.
Внимательный читатель может сказать — а как же потери площади на границе пучка? Визуально они больше, чем потери внутри пучка. Это действительно так. Но! Во-первых, это никоим образом не отменяет того, что мы получаем оценку сверху — как оценка сверху, она остается справедливой — ведь если потери площади на границах больше, то труб войдет немного меньше, чем мы рассчитали. Во-вторых, а насколько эти потери больше? Можно ли это оценить? Этим я сейчас и займусь.
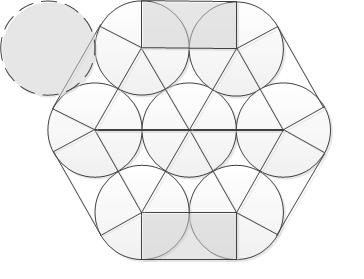
Итак, плотно упакованный пучок (кстати, то, что самой плотной упаковкой является вариант, при котором каждая окружность окружена шестью другими, доказано математически) можно представить как упакованные треугольники и упакованные прямоугольники, плюс одна окружность, образованная сгибами.
Потери площади в прямоугольниках, действительно, больше. Применяя те же самые рассуждения, получаем, что отношение полезной и общей площади . Величина опять постоянная, и их можно сравнить — полезной площади в прямоугольнике меньше в
раз.
То есть, общую площадь пучка заполняют треугольники с соотношением полезной площади , прямоугольники с соотношением полезной площади
и еще одна «полезная» окружность. Таким образом, общая полезная площадь, исходя из которой можно найти число труб в пучке состоит из
Честно говоря, думать о том, как найти общую площадь треугольников и общую площадь прямоугольников было уже лень, но представляется очевидным, что с увеличением радиуса пучка число прямоугольников растет пропорционально длине окружности, а значит, радиусу, а вот число треугольников растет пропорционально площади окружности, а значит, квадрату радиуса — то есть быстрее. Отсюда следует, что при достаточно большом (по сравнению с радиусом одной окружности) общем радиусе пучка прямоугольной составляющей можно пренебречь, точнее, считать ее потери равными потерям треугольной составляющей, и тогда полезная площадь в пучке будет равна
, а число труб в пучке, соответственно
, которое смело можно округлять до ближайшего большего. Все ж таки оценка сверху.
Напомним, что речь идет о большом пучке, так как в маленьком (см. последнюю картинку) опоясывающая «веревка» вовсе не приближается по форме к окружности, то чем больше пучок по сравнению с одной окружностью, тем ближе его форма к одной большой окружности — такое вот упрощение.
Мне тут обещали пересчитать трубы и сравнить практику с теорией — теперь буду ждать.
Комментарии