PLANETCALC Онлайн калькуляторы

Войти
УчебаМатематикаГеометрия

Расчет треугольника по координатам вершин

Этот онлайн калькулятор по введенным координатам вершин вычисляет параметры треугольника: длины сторон, углы, периметр и площадь.

Эта страница существует благодаря следующим персонам

Timur

Timur

Создан: 2021-08-12 03:43:25, Последнее изменение: 2021-08-12 03:57:32
Creative Commons Attribution/Share-Alike License 3.0 (Unported)

Этот материал распространяется на условиях лицензии Creative Commons Attribution/Share-Alike License 3.0 (Unported). Это означает, что вы можете размещать этот контент на своем сайте или создавать на его основе собственный (в том числе и в коммерческих целях), при условии сохранения оригинального лицензионного соглашения. Кроме того, Вы должны отметить автора этой работы, путем размещения HTML ссылки на оригинал работы https://planetcalc.ru/9423/. Пожалуйста оставьте без изменения все ссылки на других авторов данной работы или работы, на основе которой создана данная работа (если таковые имеются в спроводительном тексте).

Этот онлайн калькулятор предназначен для быстрого вычисления ряда характеристик треугольника по координатам его вершин. Вы вводите координаты вершин A, B и C. Калькулятор рассчитывает по координатам следующие величины:

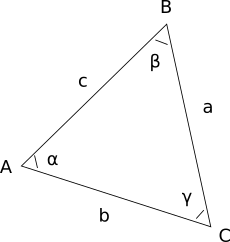
Обозначения треугольника
Обозначения треугольника

  • длину стороны a - стороны, противолежащей вершине А
  • длину стороны b - стороны, противолежащей вершине B
  • длину стороны c - стороны, противолежащей вершине C
  • значение угла α при вершине A
  • значение угла β при вершине B
  • значение угла γ при вершине C
  • периметр треугольника
  • площадь треугольника

Если нужно что-то еще, пишите в комментариях, добавим. Формулы расчета значений треугольника описаны под калькулятором.

PLANETCALC, Параметры треугольника по координатам вершин

Параметры треугольника по координатам вершин

Вершина А

Вершина B

Вершина C

Знаков после запятой: 2
Сторона a
 
Сторона b
 
Сторона c
 
Угол α
 
Угол β
 
Угол γ
 
Периметр
 
Площадь
 

Расчет треугольника по координатам вершин

Длины сторон находятся по формуле вычисления расстояния между точками в декартовых координатах
c=l_{AB}=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}

Углы - из формул скалярного произведения векторов при вершинах.
\mathbf {a} \cdot \mathbf {b} =\|\mathbf {a} \|\ \|\mathbf {b} \|\cos \gamma

Периметр находится простым суммированием длин сторон.
P=a+b+c

Площадь треугольника находится через определитель
S=\pm \frac{1}{2} \left| \begin{matrix} x_1 - x_3 & y_1 - y_3 \\ x_2 - x_3 & y_2 - y_3 \end{matrix} \right|=\pm \frac{1}{2} \left( (x_1 - x_3)(y_2 - y_3) - (y_1 - y_3)(x_2 - x_3) \right)

Ссылка скопирована в буфер обмена

Похожие калькуляторы

 Геометрия периметр площадь треугольник
PLANETCALC, Расчет треугольника по координатам вершин
Timur2021-08-12 03:57:32

Комментарии