Построение эпюр внутренних усилий
Калькулятор строит эпюры поперечных сил и моментов в простой балке под воздействием различных нагрузок.
Этот материал распространяется на условиях лицензии Creative Commons Attribution/Share-Alike License 3.0 (Unported). Это означает, что вы можете размещать этот контент на своем сайте или создавать на его основе собственный (в том числе и в коммерческих целях), при условии сохранения оригинального лицензионного соглашения. Кроме того, Вы должны отметить автора этой работы, путем размещения HTML ссылки на оригинал работы https://planetcalc.ru/9401/. Пожалуйста оставьте без изменения все ссылки на других авторов данной работы или работы, на основе которой создана данная работа (если таковые имеются в спроводительном тексте).
Данный онлайн калькулятор предназначен для построения эпюр внутренних усилий. Эпюра внутренних усилий - график, показывающий характер изменения внутренних усилий по длине стержня. Построение эпюр необходимо для определения положения наиболее нагруженного (опасного) сечения стержня. Калькулятор наглядно изображает эпюру изгибающего момента M и поперечной силы Q. Теорию и формулы расчета можно найти ниже под калькулятором.
Нагрузка
| Расстояние от опоры A | Нагрузка | Значение | Направление | Направление момента | Протяженность | Изменение | ||
|---|---|---|---|---|---|---|---|---|
Внутренние силы
Для иллюстрации внутренних сил, действующих в балке под нагрузкой, рассмотрим следующий рисунок.
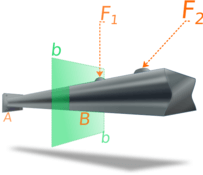
Мысленно рассечем балку на два сегмента в точке B, где мы будем определять внутренние силы, действующие в балке.
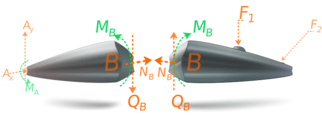
Внутренние силы, действующие в сечении балки можно показать как внешние, на диаграмме свободного тела рассеченной балки. Компонента NB, действующая вдоль балки, называется нормальной силой. В калькуляторе мы не рассматриваем нормальную силу, так как можно ввести только поперечные нагрузки.
Компонента внутренних сил QB, действующая параллельно сечению называется поперечной силой. На рисунке отражена только y-составляющая поперечных сил, в действительности возможна еще и z-составляющая. Калькулятор не допускает поворота нагрузки вокруг оси x, поэтому в наших вычислениях эта составляющая отсутствует.
Моменты MB называются изгибающими моментами. Изгибающий момент равен сумме моментов всех внешних сил, приложенных к рассматриваемой части балки, относительно центра тяжести проведенного сечения.
Компоненты сил препятствуют относительному смещению двух сегментов, моменты препятствуют относительному вращению.1
Построение эпюр методом интегрирования.
Мы будем искать формулы для вычисления значений поперечной силы Q(x) и изгибающего момента M(x) отдельно для разных участков балки.
Границами участков являются характерные точки: концевые сечения балки, точки опор, точки приложения сосредоточенных сил и моментов, точки начала и конца действия распределенных нагрузок.
Для каждого участка, вычисляется интеграл от функции распределенной нагрузки q(x) для определения поперечной силы Q(x), следующим шагом вычисляется интеграл от Q(x) для определения функции изгибающего момента M(x) в соответствии с формулами:
Распределенная нагрузка q(x) в нашем калькуляторе может быть линейной, равномерно убывающей или возрастающей. В первом случае q(x) - константа , во втором - линейная функция: kx+b, в случае отсутствия распределенных нагрузок на участке q(x)=0, поперечная сила будет равна константе.
Таким образом для отыскания функций Q(x) и M(x) потребуется вычисление неопределенного интеграла от многочлена и вычисление константы интегрирования. Константу интегрирования можно найти, зная какую либо точку, через которую проходит искомая функция. См.: Интеграл многочлена.
В качестве такой точки будем брать значения Q(x) и M(x) по левой границе участка.
Q(xl) будет равно значению функции поперечной силы Q(x) для предыдущего участка в точке l, смещенное на величину сосредоточенной силы (или опорной реакции) в этой точке. Если сила действует вверх, то смещение положительно, если вниз - отрицательно.
M(xl) будет равно значению функции изгибающего момента M(x) для предыдущего участка в точке l, смещенное на величину сосредоточенного момента, приложенного к этой точке. Если сосредоточенный момент направлен по часовой стрелке, то смещение положительно, в противном случае - отрицательно.
Значение Q(x) на левом краю балки будет соответствовать сумме сосредоточенных сил и опорной реакции в этой точке, или будет равно нулю при отсутствии таковых. Значение M(x) по краям балки равно сумме значений сосредоточенных моментов приложенных к концам балки. Если сосредоточенных моментов в этих точках нет, то M(x) будет равен нулю.
Знаки для М(x) и Q(x) можно связать с характером деформации балки при действии внешних сил. Если изгибающий момент в сечении положителен, то балка в этом сечении гнется выпуклостью вниз, если же он отрицателен, то балка гнется выпуклостью вверх.
Пример
Рассмотрим получение функций Q(x) и M(x) на примере:
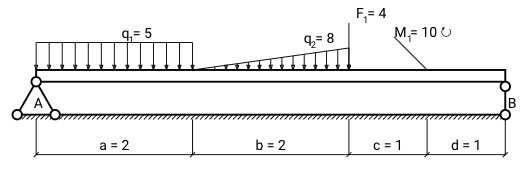
- Первым делом вычисляются реакции опор. Посмотреть как они находятся можно в этом калькуляторе.
Получаем реакции опор:
- Балка делится на участки по ключевым точкам с координатами: 0, 2, 4, 5, 6.
Участок А - характерные точки 0,2
Участок B - характерные точки 2,4
Участок C - характерные точки 4,5
Участок D - характерные точки 5,6 - Для каждого участка находим формулу распределенной нагрузки, интегрируем ее дважды получая формулу для поперечных сил Q(x) и изгибающих моментов M(x). Константы интегрирования вычисляются по левой границе участка по формулам для предыдущих участков.
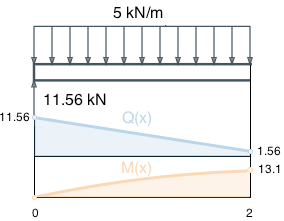
Участок А, значения в характерных точках Участок А
Распределенная нагрузка на участке равна: q(x) = 5. Найдем функцию поперечной силы на участке, путем интегрирования функции распределенной нагрузки:
Выразим константу C = Q(x)+5x, и подставим в формулу x=0 и значение поперечной силы в этой точке. Поперечная сила на концах балки равна нулю, но в точке 0 она изменена реакцией опоры VA=11.56кН, которая направленна вверх. Соответственно поперечная сила в точке 0 будет равна Q(0) = 0 + 11.56 = 11.56.
Поэтому C = 11.56 - 5 ⋅ 0 = 11.56
Формула для поперечной силы на участке А:
Интегрируя функцию поперечной силы, получаем функцию изгибающего момента:
Аналогичным образом, значение момента на концах балок = 0, сосредоточенных моментов в начальной точке нет, поэтому M(0) = 0.
Подставляя x=0 и M(0) = 0 в выражение для C = M(x) + 2.5x2 - 11.56x = 0 + 2.5 · 02 - 11.56 · 0 получаем значение C = 0
Формула для изгибающего момента на участке А:
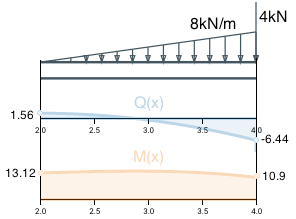
Участок B
Чтобы найти распределенную нагрузку q(x) воспользуемся уравнением прямой линии по двум точкам.
По точкам (2;0) и (4;8) получаем уравнение для распределенной нагрузки: q(x) = 4x-8.
Найдем функцию поперечной силы на участке, интегрируя полученную функцию распределенной нагрузки.
По формуле Q(x) для предыдущего участка вычисляем значение Q на левой границе участка: Q(2)=-5∙2+11.56 = 1.56. Аналогично, как и на предыдущем участке вычисляем интеграл и константу интегрирования по точке (2;1.56).
Получим формулу для поперечной силы на участке B:
см. расчет
По формуле из предыдущего участка вычислим значение момента на левой границе участка: M(2) = -2.5 ∙ 22 + 11.56 ∙ 2 + 0= 13.12 .
Интегрируя формулу Q(x) и вычисляя константу интегрирования по граничной точке получим формулу для изгибающего момента на участке B:
см. расчет
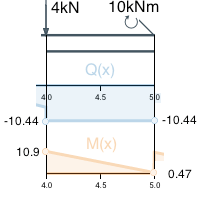
Участок C
По формуле Q(x) для предыдущего участка вычисляем значение Q на левой границе участка: Q(4) = -2 ∙ 42 + 8 ∙ 4 – 6.44 = -6.44.
Сосредоточенная сила скачком изменяет Qx в данной точке, она направлена вниз и потому отрицательна: Q(4) = -6.44 - 4 = -10.44
На третьем участке нет распределенной нагрузки, поперечная сила равна константе по последней точке.
Получим формулу для поперечной силы на участке С:
По формуле из предыдущего участка вычислим значение момента на левой границе участка: M(4) = -0.67 ∙ 43 + 4 ∙ 42 – 6.44 ∙ 4 + 15.33 = 10.91
Интегрируя формулу Q(x) и вычисляя константу интегрирования по граничной точке получим формулу для изгибающего момента на участке С:
см. расчет
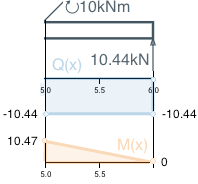
Участок D
К данному участку также не приложена распределенная нагрузка, поперечная сила равна константе.
Формула для поперечной силы на участке D:
По формуле из предыдущего участка вычислим значение момента на левой границе участка: M(5) = -10.44 ∙ 5 + 52.67 = 0.47
Сосредоточенный момент скачком изменяет Mx в данной точке, он направлен по ходу часовой стрелки и поэтому положителен: M(5) = 0.47 + 10 = 10.47
Интегрируя формулу Q(x) и вычисляя константу интегрирования по граничной точке получим формулу для изгибающего момента на участке D:
см. расчет
Чтобы проверить правильность формул найдем значения поперечной силы и изгибающего момента в крайней точке балки.
Сосредоточенная сила в данной точке по величине равна опорной реакции с противоположным знаком. Изгибающий момент на концах балки равен нулю.
Комментарии