PLANETCALC Онлайн калькуляторы

Войти
УчебаМатематикаГеометрия

Превышение по горизонтальному проложению и углу наклона с учетом погрешности измерений

Этот онлайн калькулятор позволяет рассчитать превышение с учетом средней квадратической погрешности измерения горизонтального проложения и угла наклона.

Эта страница существует благодаря следующим персонам

Timur

Timur

Создан: 2021-01-05 08:55:59, Последнее изменение: 2021-01-05 09:01:26
Creative Commons Attribution/Share-Alike License 3.0 (Unported)

Этот материал распространяется на условиях лицензии Creative Commons Attribution/Share-Alike License 3.0 (Unported). Это означает, что вы можете размещать этот контент на своем сайте или создавать на его основе собственный (в том числе и в коммерческих целях), при условии сохранения оригинального лицензионного соглашения. Кроме того, Вы должны отметить автора этой работы, путем размещения HTML ссылки на оригинал работы https://planetcalc.ru/9093/. Пожалуйста оставьте без изменения все ссылки на других авторов данной работы или работы, на основе которой создана данная работа (если таковые имеются в спроводительном тексте).

Данный калькулятор вычисляет превышение по горизонтальному проложению и углу наклона, а также среднюю квадратическую погрешность определения превышения с учетом средней квадратической погрешности определения горизонтального проложения и угла наклона. Формулы расчета приведены под калькулятором

PLANETCALC, Вычисление превышения по горизонтальному проложению и углу наклона с учетом погрешности измерений

Вычисление превышения по горизонтальному проложению и углу наклона с учетом погрешности измерений

°
′
″
°
′
″
Знаков после запятой: 2
Превышение, метры
 
СКП превышения, метры
 

Вычисление превышения

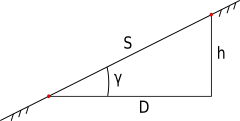
На рисунке ниже используются следующие обозначения:

  • S - длина линии
  • D - горизонтальное проложение линии, т.е. проекция линии местности на горизонтальную плоскость.
  • h - превышение, т.е. разность высот одной точки относительно другой точки
  • γ - угол наклона линии к горизонту

Горизонтальное проложение
Горизонтальное проложение



Из достаточно очевидных геометрических соображений превышение можно выразить через горизонтальное проложение и угол наклона к горизонту следующей формулой:
h = D tg \gamma

Средняя квадратическая погрешность измерения

Точность измерения каких-либо величин характеризуется средней квадратической погрешностью (СКП) измерения. Для величин, измеренных явно, СКП, как правило, известны. Превышение измеряется косвенно, в данном случае, его величина рассчитывается как функция от горизонтального проложения и угла наклона.

Общая формула зависимости СКП результата вычисления функции от СКП ее аргументов выглядит следующим образом:

Если величина y вычисляется как функция от аргументов x_1, x_2, ..., x_n, характеризующихся СКП m_{x_1}, m_{x_1},..., m_{x_1}:
y = f(x_1, x_2, ..., x_n)

то СКП определения величины y равно:
m_y=\sqrt{ \left(\frac{\delta f}{\delta x_1}\right)^2_0m^2_{x_1} + \left(\frac{\delta f}{\delta x_2}\right)^2_0m^2_{x_2} + ... + \left(\frac{\delta f}{\delta x_n}\right)^2_0m^2_{x_n} }

где \frac{\delta f}{\delta x_k} - частная производная функции по переменной x_k. Индекс 0 обозначает, что берется численное значение частной производной, полученное после подстановки численных значений аргументов.

В случае функции h = D tg \gamma мы имеем

m_h=\sqrt{ \left(\frac{\delta h}{\delta D}\right)^2_0m^2_{D} + \left(\frac{\delta h}{\delta \gamma}\right)^2_0m^2_{\gamma}} = \sqrt{ tg^2\gamma m^2_{D} + \left(\frac{D}{cos^2 \gamma}\right)^2 m^2_{\gamma}}

Угол наклона и СКП угла наклона должно быть выражено в радианах.

Эта формула и используется в калькуляторе для определения СКП превышения.

Ссылка скопирована в буфер обмена

Похожие калькуляторы

 геодезия Геометрия горизонтальное проложение измерение погрешность превышение средняя квадратическая погрешность
PLANETCALC, Превышение по горизонтальному проложению и углу наклона с учетом погрешности измерений
Timur2021-01-05 09:01:26

Комментарии