Как определить лежит ли точка внутри треугольника или снаружи.

Этот калькулятор определит где находится заданная точка внутри 2-мерного треугольника или вовне. Калькулятор использует простой алгоритм, основанный на свойствах векторного произведения. Описание этого алгоритма можно найти сразу за калькулятором.

Точка в треугольнике

Вершина A

Вершина B

Вершина C

Точка P

Точность вычисления

Знаков после запятой: 2

Рассчитать

Точка вниутри треугольника?

 

Векторное произведение ( z - координата )

AB x AP

 

BC x BP

 

CA x CP

 

 Ссылка  Сохранить  Виджет

Точка внутри треугольника. Описание алгоритма.

Векторное произведение векторов a и b, заданного декартовыми координатами в пространстве для 3-х мерного правого ортонормального базиса можно выразить так:
[1].
Векторное произведение обладает свойством антикоммутативности:

Это важное свойство мы будем использовать для решения нашей задачи.

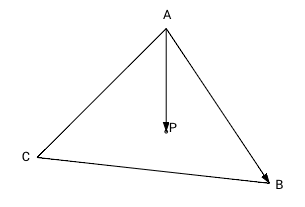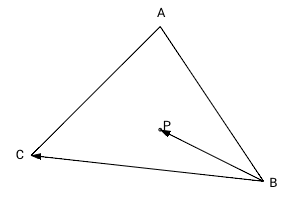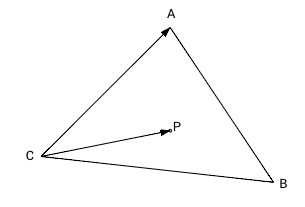
Для того чтобы определить лежит ли точка P внутри треугольника ABC мы вычислим 3 векторных произведения: ABxAP, BCxBP and CAxCP. Так как наш треугольник и точка в 2-мерном пространстве на плоскости, третья координата z для трехмерного пространства равна нулю. Согласно формуле [1] мы можем не вычислять координаты x и y для векторного произведения, если координата z векторов-множителей равна нулю - координаты x и y результата в этом случае всегда равны нулю (результирующий псевдо-вектор перпендикулярен плоскости треугольника). Знак результата произведения для оставшейся координаты (z) зависит от относительного положения умножаемых векторов. Если первый вектор (в нашем случае это сторона треугольника) находится правее второго вектора (вектор из вершины в точку P), то координата z результата будет положительна, если первый вектор будет левее второго - отрицательна, и в противном случае, если оба вектора идут в одном и том же направлении, результат будет равен нулю.
Получив результаты по трем векторным произведениям, нам остается их проанализировать, чтобы понять лежит ли точка внутри треугольника:
Если мы имеем и положительные и отрицательные результаты, точка лежит вне треугольника, если результаты только положительные или только отрицательные, точка - внутри.
Таблица далее иллюстрирует все возможные варианты результатов векторного произведения:

Рисунок	Описание
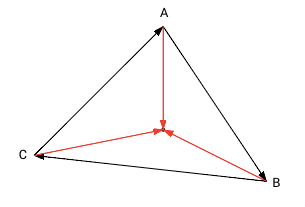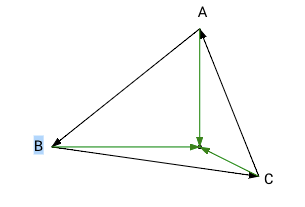	Все результаты положительные или все результаты отрицательные. Точка - внутри треугольника.
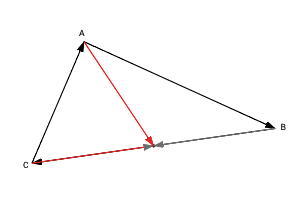	Один результат равен нулю, остальные все либо положительны, либо все отрицательны. Точка лежит на стороне треугольника. Если два результата равны нулю, точка совпадает с вершиной треугольника.
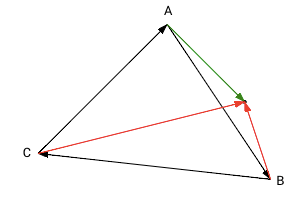	Если имеются и положительные и отрицательные результаты. Точка лежит вне треугольника.