Угловой размер, линейный размер и расстояние
Калькуляторы рассчитвающие параметры по соотношениям между угловым размером тела, линейным размером тела и расстоянием до тела.
Эта страница существует благодаря следующим персонам
 | Timur
|
Этот материал распространяется на условиях лицензии Creative Commons Attribution/Share-Alike License 3.0 (Unported). Это означает, что вы можете размещать этот контент на своем сайте или создавать на его основе собственный (в том числе и в коммерческих целях), при условии сохранения оригинального лицензионного соглашения. Кроме того, Вы должны отметить автора этой работы, путем размещения HTML ссылки на оригинал работы https://planetcalc.ru/1897/. Пожалуйста оставьте без изменения все ссылки на других авторов данной работы или работы, на основе которой создана данная работа (если таковые имеются в спроводительном тексте).
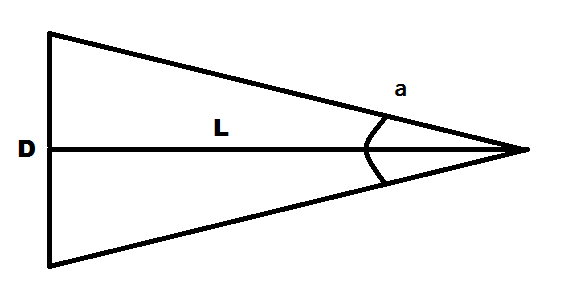
Угловой размер — это угол между линиями, соединяющими диаметрально противоположные точки измеряемого объекта и глаз наблюдателя.
Посмотрим на рисунок: здесь отрезок D — измеряемый объект, отрезок L — линия наблюдения, перпендикулярная отрезку D и являющаяся его серединным перпендикуляром, и угол а — угловой размер отрезка D.
Очевидные соотношения между величинами (вспомним тригонометрию):
Таким образом, наблюдатель, зная, например, линейный размер объекта, по угловому размеру объекта может определить расстояние до него. Помню, раньше для этих целей военные бинокли снабжали специальными риcками для определения углового размера.
Ну и обратные задачи тоже имеют место — зная, например, расстояние и линейный размер объекта, можно определить его угловой размер; и наконец, зная расстояние и угловой размер, можно определить линейный размер. Последние задачи актуальны для астрономии. Там используют термин угловой диаметр — то есть видимый диаметр небесного тела, выраженный в угловых мерах.
Ниже калькуляторы, рассчитывающие неизвестные по всем соотношениям. В качестве данных по умолчанию используется расстояние от Земли до Солнца, диаметр Солнца и средний угловой диаметр Солнца, наблюдаемого с Земли.
Расстояние по угловому и линейному размеру
Линейный размер по угловому размеру и расстоянию
Комментарии