Уравнивание линейно-угловой сети параметрическим способом
Этот онлайн калькулятор предназначен для проверки решения задачи №3 на уравнивание линейно-угловой сети параметрическим способом из раздела $3.2 "Параметрический способ уравнивания" учебника В.В. Голубева "Геодезия. Теория математической обработки геодезических измерений"
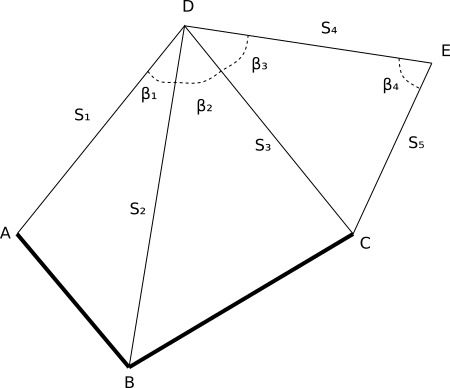
Задача звучит следующим образом1: На рисунке приведена линейно-угловая сеть. Измерены углы и стороны. Измерения проводились тахеометром, обеспечивающим точность измерения углов со средним квадратическим отклонением 5'' и сторон со средним квадратическим отклонением 1 см. Уравнять данную сеть параметрическим способом. Произвести оценку точности уравненных координат, измерений и функцию, которую задаст преподаватель.
Процесс уравнивания описан в параграфе 3.2. Калькулятор повторяет процесс уравнивания, выводя результаты промежуточных шагов для проверки вычислений. Обратите внимание, что приближенные координаты пункта E вычисляются от пункта С, для чего и находится дирекционный угол стороны CE. Также по опыту стоит заметить, что большинство ошибок допускается при определении дирекционных углов измеренных сторон. Рекомендую делать примерный рисунок точек, из которого будет понятно взаимное расположение их относительно друг друга, а для сверки можно использовать таблицу "Дирекционные углы".
В качестве функции, для которой производится оценка точности, взята функция дирекционного угла стороны EC.
Определение дирекционного угла AD
Приближенные координаты точки D
Определение дирекционного угла CE
Приближенные координаты точки E
-
Голубев В.В. Геодезия. Теория математической обработки геодезических измерений: учебник для вузов. -М.: Изд-во МИИГАиК, 2016. - 422 с.: ил. - стр. 398 ↩
Похожие калькуляторы
- • Решение задачи на уравнивание линейно-угловой сети параметрическим способом по вариантам
- • Переход между плоскими прямоугольными координатами Гаусса и географическими координатами и обратно
- • Радиус Земли по широте (WGS 84)
- • Расстояние между двумя координатами сквозь Землю
- • Скорость при равноускоренном движении в релятивистской механике
- • Раздел: Учеба ( 434 калькуляторов )
Комментарии