Трилатерация
Этот онлайн калькулятор решает задачу трилатерации - определения координат точки по расстоянию от этой точки до трех других точек с известными координатами.
Этот материал распространяется на условиях лицензии Creative Commons Attribution/Share-Alike License 3.0 (Unported). Это означает, что вы можете размещать этот контент на своем сайте или создавать на его основе собственный (в том числе и в коммерческих целях), при условии сохранения оригинального лицензионного соглашения. Кроме того, Вы должны отметить автора этой работы, путем размещения HTML ссылки на оригинал работы https://planetcalc.ru/10159/. Пожалуйста оставьте без изменения все ссылки на других авторов данной работы или работы, на основе которой создана данная работа (если таковые имеются в спроводительном тексте).
Результатом решения задачи может быть один из трех вариантов:
- Не существует ни одной точки, расстояния от которой до трех других соответствуют заданным
- Существует ровно одна точка, расстояния от которой до трех других соответствуют заданным
- Существует две точки, расстояния от которых до трех других соответствуют заданным
Формулы расчета и иллюстрации для каждого случая приведены под калькулятором.
Трилатерация
Геометрическим местом точек, лежащих на заданном расстоянии r от точки с координатами (x, y, z) является поверхность сферы радиуса r с центром в точке (x, y, z). Таким образом с точки зрения геометрии проблема трилатерации заключается в нахождении координат пересечения трех сфер. Эти координаты находятся путем решения системы уравнений, построенных на следующих рассуждениях1.
Каждая пара сфер пересекается по окружности. Центр ее находится на прямой, соединяющей центры сфер. Сама окружность лежит в плоскости, перпендикулярной данной прямой. Рассмотрим три сферы: сферу 1 с радиусом r1 c центром в точке O1(x1, y1, z1), сферу 2 с радиусом r2 c центром в точке O2(x2, y2, z2) и сферу 3 с радиусом r3 c центром в точке O3(x3, y3, z3).
Уравнение плоскости, в которой лежит окружность, образованная пересечением сфер 1 и 2 выглядит следующим образом:
Уравнение плоскости, в которой лежит окружность, образованная пересечением сфер 1 и 3 выглядит следующим образом:
Уравнение плоскости треугольника, образованного центрами сфер:
Пересечение двух первых плоскостей дает прямую, перпендикулярную последней плоскости. Пересечение этой прямой с плоскостью треугольника - перпендикуляр из искомой точки пересечения сфер на плоскость треугольника, образованного центрами сфер. Эта точка пересечения принадлежит всем трем плоскостям, и ее координаты являются решением системы трех линейных алгебраических уравнений, приведенных выше.
Решив эту систему, получаем координаты точки O (x0, y0, z0).
Тогда координаты точки пересечения трех сфер определяются следующими формулами:
Выражение для расчета k определяет количество решений. Если разность под квадратным корнем положительная, то мы имеем два решения (+k, -k) - две точки пересечения трех сфер, проиллюстрированных картинкой ниже
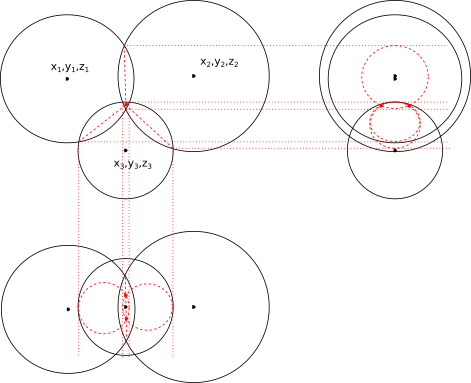
Если разность под корнем равна нулю, то мы имеем в точности одну точку пересечения двух сфер:
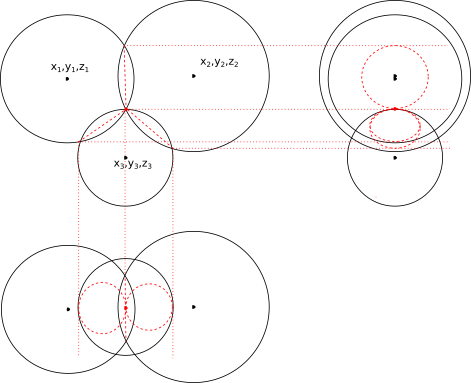
И наконец, если выражение под корнем отрицательное, то решений нет - сферы не пересекаются
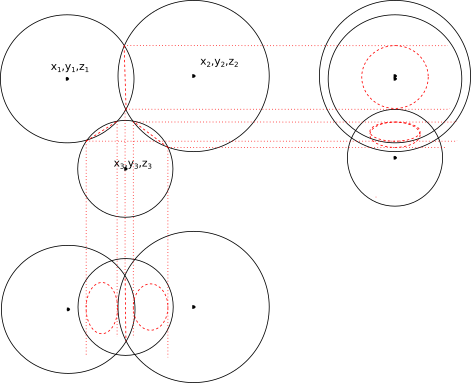
Комментарии