Конденсатор в цепи постоянного тока
Калькуляторы рассчитывают параметры разрядки и зарядки конденсатора от источника постоянной ЭДС через сопротивление.
Калькуляторы рассчитывают параметры разрядки и зарядки конденсатора от источника постоянной ЭДС через сопротивление. Формулы, по которым идет расчет, приведены под калькуляторами.
Понять приводимые ниже формулы поможет картинка, изображающая электрическую схему заряда конденсатора от источника постоянной ЭДС (батареи):
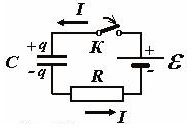
Итак, при замыкании ключа К в цепи пойдет электрический ток, который будет приводить к заряду конденсатора.
По закону Ома сумма напряжений на конденсаторе и резисторе равна ЭДС источника, таким образом:
При этом заряд и сила тока зависят от времени. В начальный момент времени на конденсаторе нет заряда, сила тока максимальна, также как и максимальна мощность, рассеиваемая на резисторе.
Во время зарядки конденсатора, напряжение на нем изменяется по закону
где величину
называют постоянной времени RC-цепи или временем зарядки конденсатора.
Вообще говоря, согласно уравнению выше, заряд конденсатора бесконечно долго стремится к величине ЭДС, поэтому для оценки времени заряда конденсатора используют величину
— это время, за которое напряжение на конденсаторе достигнет значения 99,2% ЭДС.
Заряд на конденсаторе:
Энергия, запасенная в конденсаторе:
Работа, выполненная источником ЭДС:
Комментарии