Онлайн калькулятор: Вычисление объема амфоры

Метод требует серии измерений внутреннего радиуса сосуда на разном расстояний от горла, желательно с равномерным шагом, см. картинку.

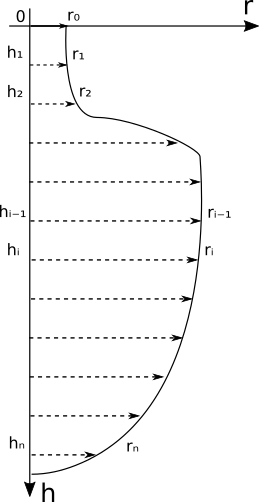
Результаты вводятся в таблицу ниже, в виде пар чисел "расстояние от горла" - "внутренний радиус". Описание метода, используемого калькулятором, а также обзор других методов расчета объема амфор, можно найти под калькулятором.

Вычисление объема амфоры

Размеры амфоры

	Глубина от горлышка, см	Внутренний радиус, см

Оценка снизу, л

Рассчитанный объем, л

Оценка сверху, л

Точность вычисления

Знаков после запятой: 2

Показать профиль амфоры

Профиль амфоры

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.

Методы расчета объемов амфор

Амфоры широко использовались во времена античности для торгового обмена. В амфорах перевозили и жидкости (вино, масло), и сыпучие товары (зерно). Расчеты объема амфор позволяют оценить размер торговли. Но помимо этого, объем является одной из характеристик амфоры, которые позволяют установить ее место происхождения, так как для различных центров производства были характерны свои "амфорные стандарты".

Естественно, там, где это возможно, археологи пытаются провести фактические измерения, заполняя амфоры жидкостью или сыпучими телами. Понятно, что это касается только амфор без дефектов корпуса. В остальных случаях надо как-то считать.

Хорошую обзорную статью 2008 года, посвященную методам расчета объемов амфор, используемых современными археологами, можно найти у Л.Н. Водолажской¹.
С 1864 года² известна так называемая формула Герона Александрийского для объема пифоида:
$V_{Her}=\frac{11}{14}\cdot\left(\frac{d_{max}+d_{min}}{2}\right)^2 \cdot H$
В середине 20-го века ее предложили использовать для расчета объемов определенных типов амфор (которые назвали "пифоидные амфоры")
Общепринятая интерпретация формулы:
$d_{min}$ - максимальный диаметр тела амфоры
$d_{max}$ - диаметр устья горла амфоры
$H$ - глубина амфоры.
Некоторые исследователи интерпретируют множитель $\frac{11}{14}$ как $\frac{\pi}{6}$ . Также упоминается модификация этой формулы для "сфероидного пифоса":
$V_{Her}=\frac{11}{21}\cdot\left(\frac{d_{max}+d_{min}}{2}\right)^2 \cdot H$

Эти формулы не универсальны, поэтому существует большое количество других формул, подобранных различными исследователями, исходя из типа амфоры, и некоторой физической интерпретации ее размеров. За подробностями я отсылаю к вышеприведенной статье, а для понимания как это выглядит, в качестве примера приведу формулу, предложенную С.Ю. Монаховым в 1986 году³:
$V = K \cdot H_4 \cdot D_{av}^2$
где
$H_4$ - разница между глубиной сосуда и высотой горла (горло начинается от места максимального диаметра амфоры)
$D_{av}$ - средний диаметр амфоры (среднее арифметическое между максимальным диаметром и диаметром горла)
а вот коэффициент K зависит от типа амфоры. Монахов выделил "пифоидные" амфоры с K=1 и средней точностью расчета 4%, "конические" амфоры с K=11/14 и точностью 13%, и "шаровидные" амфоры с K=8/7 и точностью 7%.

Главное тут то, что исследователи в большинстве случаев, видимо, для упрощения себе жизни, пытаются создать формулу для расчета объема амфор эмпирически, исходя из того типа амфор, с которым они работают на данный момент, и пытаясь рассчитывать их объемы через объемы простых геометрических тел (конусов и параллелепипедов), чьи размеры каким-то образом связываются с определенными размерами амфор.

Сама Л.Н. Водолажская описывает метод расчета объема через построение математической модели амфоры, как сложного тела вращения, полученного геометрической аппроксимацией. В этом методе амфора разделяется на три сегмента: тулово, плечи и горло. Профиль тулова аппроксимируется усеченной параболой, и рассчитывается объем усеченного параболоида вращения, профиль плеч аппроксимируется усеченным эллипсом, и объем находится как объем половины усеченного эллипсоида вращения, и, наконец, профиль горла опять-таки аппроксимируется параболой, однако объем рассчитывается с учетом того, что ось вращения тела находится с внешней стороны от оси симметрии параболы.

Метод расчета был апробирован на выборке из 60 амфор с неповрежденной емкостной частью объемами от 2,6 до 4,2 литра, при этом максимальное отклонение от объемов, измеренных водой или зерном составляло 6%, со средним отклонением в 3%, что считается высокой степенью соответствия математической модели реальным амфорам.

Математическая модель эта, однако, касается только узкогорлых светлоглиняных амфор III в.н.э из Танаиса, и, как пишет Л.Н. Водолажская: "Каждый тип амфор требует индивидуального рассмотрения с точки зрения математического моделирования их формы и требует индивидуального вывода и апробации формул для расчета их объема."

В отличие от рассмотренных эмпирических формул и формул Герона, калькулятор выше использует достаточно универсальную методику, предложенную О.О.Барабановой и С.Б.Платоновым в 1982 году⁴. Суть методики состоит в следующем: диаметр амфоры замеряется через определенный интервал, как правило, через каждые 3-4 сантиметра. Таким образом тело амфоры разбивается на определенное количество частей, каждую из которых можно представить как цилиндр. При этом радиус цилиндра каждой части можно определять тремя способами: по минимальному из двух, по максимальному из двух, и по среднему из двух (см. рис.).

Построение цилиндров: по минимальному радиусу, по среднему радиусу, по максимальному радиусу

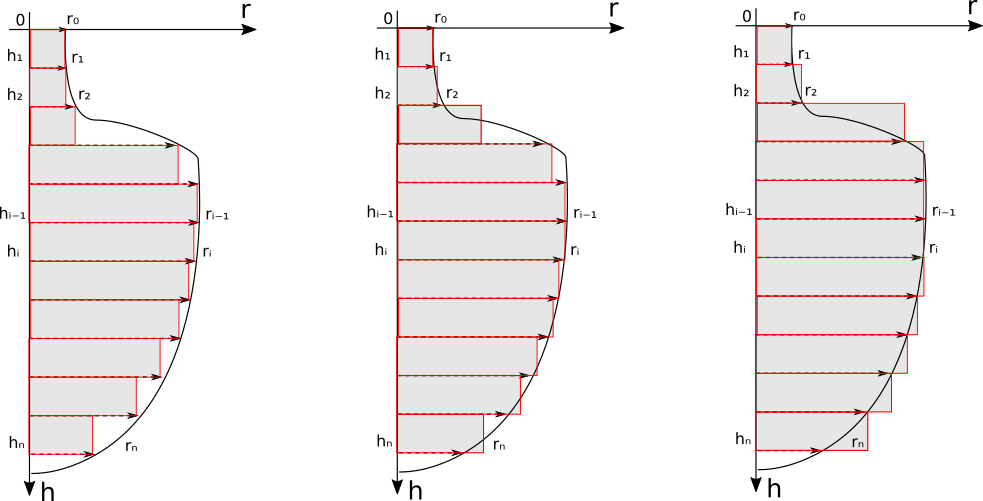
Формула объема для расчета по среднему радиусу будет выглядеть так:
$V=\sum_{i=1}^n \pi \left(\frac{r_{i-1}+r_{i}}{2} \right)^2 \cdot \left(h_i - h_{i-1} \right)$
Если эта формула вам что-то смутно напоминает из курса математики, то вы не ошиблись. По сути это численное интегрирование табличной функции методом трапеций
$\int _{a}^{b}f(x)\,dx\approx \sum _{{i=0}}^{{n-1}}{\frac {f(x_{i})+f(x_{{i+1}})}{2}}(x_{{i+1}}-x_{{i}})$
Здесь x - это глубина, а f(x) - значение, вычисленное как $\pi r^2$ (площадь окружности) для радиуса, соответствующего глубине.

Формулы для объемов, полученных на минимальных и максимальных радиусах выглядят так:
$V_{min}=\sum_{i=1}^n \pi \cdot min(r_{i-1}, r_{i}})^2 \cdot \left(h_i - h_{i-1} \right) \\ V_{max}=\sum_{i=1}^n \pi \cdot max(r_{i-1}, r_{i}})^2 \cdot \left(h_i - h_{i-1} \right)$
Фактически они дают оценку объема амфоры снизу и сверху.

Авторы не приводят относительную погрешность рассчитанного таким образом объема по сравнению с фактически измеренным, однако пишут что абсолютная погрешность для амфор небольших размеров достигала 0.03 литра, а для амфор средних и больших размеров - от 0.3 до 1 литра. Для понимания, минимальный объем амфоры в их выборке составлял 3.05 литра, а максимальный - около 40 литров.

Остается заметить, что некоторые исследователи предлагают для изучения объемов амфор использовать программное обеспечение для 3D моделирования, например, Autodesk 3Ds Max⁵. Основная идея заключается в том, чтобы на оцифрованной прорисовке контура амфоры "подогнать" масштабную меру под масштабную линейку 3Ds Max, прорисовать контур амфоры в 3Ds Max и рассчитать объем тела вращения, полученного по контуру. Представляется, что концептуально это примерно тоже самое, что и выполнение численного интегрирования, описанного выше, только оно выполняется при помощи компьютерной программы, и с большей точностью. Однако здесь критическим является недопущение погрешностей при подборе масштаба и оконтуривании прорисовки.

На наборе из 75 амфор Е.В. Суханов фиксирует среднее расхождение между объемами, полученными с помощью 3Ds Max, и объемами, полученными другими методами, включая метод Барабановой и Платонова, в 9-10%, причем пишет, что расхождение увеличивается до 15-20% для более выпуклых и шаровидных амфор. Вероятно это связано с тем, как именно эти амфоры разбивались на цилиндрические сегменты, но, к сожалению, автор не описывает, ни с каким шагом выполнялось разбиение, ни точность вычисления по сравнению с объемом, измеренным непосредственно.

Как представляется, использование метода Барабановой и Платонова с разбиением на большее количество сегментов может повышать точность расчета, но одновременно и увеличивать его трудоемкость. Впрочем, при использовании калькулятора выше, который берет на себя численное интегрирование, повышение трудоемкости будет заключаться только в увеличении числа замеров диаметра амфоры.

Водолажская Л.Н. К вопросу о методе расчета объема амфор // Archaeoastronomy and Ancient Technologies 2020, 8(1), 47-59 (Изначально опубликована в 2008 году в сборнике Историко-археологические исследования в Азове и на Нижнем Дону в 2006 г. Выпуск 23. - г. Азов: Издательство Азовского музея-заповедника, 2008.) ↩
Hultsch F. Metrologicorum scriptorum reliquiae. Lipsiae, 1864, Bd I, S. 202, N 19 ↩
Монахов С.Ю. О некоторых особенностях расчета стандартных мер емкости остродонных амфор // Античный мир и археология. - Саратов, 1986. - Вып.6. ↩
Барабанова О.О., Платонов С.Б. К методике изучения объемов средневековых амфор // АДСВ. Византия и ее провинции. Вып. 19 / Отв. ред. М.Я. Сюзюмов. Свердловск: Изд-во УрГУ. 1982. С. 127-133. ↩
Суханов Е.В. Использование трехмерного моделирования при изучении объемов средневековых «причерноморских» амфор // Археология и геоинформатика. Вып. 8. – М.: ИА РАН, 2017 – ISBN 978-5-94375-220-9 ↩

PLANETCALC Онлайн калькуляторы

Вычисление объема амфоры

Эта страница существует благодаря следующим персонам

Timur

Вычисление объема амфоры

Размеры амфоры

Методы расчета объемов амфор

Похожие калькуляторы

Комментарии

PLANETCALC Онлайн калькуляторы

Вычисление объема амфоры

Методы расчета объемов амфор

Похожие калькуляторы

Комментарии

Поделиться этой страницей