Синтетическое деление полиномов
Простой метод деления полиномов. Генерализация правила Руффини для делителя общего вида.
Синтетическое деление это простой способ евклидова деления полиномов с небольшим количеством записей и вычислений. Калькулятор ниже выполняет деление полиномов этим методом. Описание метода можно найти сразу под калькулятором.
Подготовка к синтетическому делению
Будем рассматривать подготовку к делению на примере: 3x4+5x3+2x+4 / x2+2x+1.
| Шаги подготовки | |
|---|---|
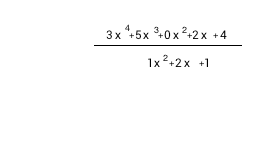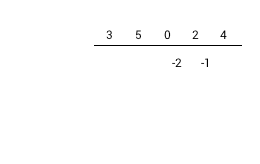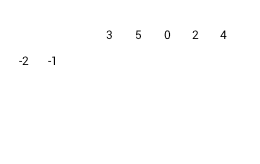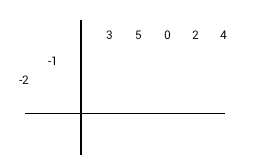 |
1) Взять коэффициенты делителя с обратным знаком. 2) Записать коэффициенты делимого в верхней строке. Если коэффициента нет - записываем ноль. 3) Отбросим коэффициент делителя самой большой степени 4) Запишем коэффициенты делителя диагонально слева. Свободный член в самом верху |
Синтетическое деление для монических делителей
Изначально метод был разработан для делителей, являющихся моническими полиномами (коэффициент старшего члена = 1). Рассмотрим деление на примере: 3x4+5x3+2x+4 / x2+2x+1.
| Алгоритм деления для монического делителя | |
|---|---|
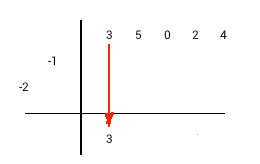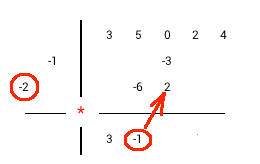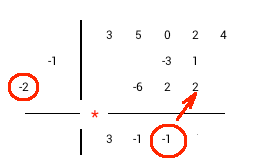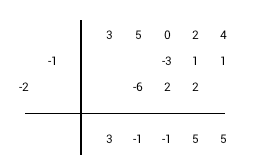 |
1) Опустим старший коэффициент делимого в строку результата 2) Умножим диагональ с коэффициентами делителя на крайний левый коэффициент из строки результатов 3) Поместим результат умножения диагонально справа от последнего столбца с результатами 4) Выполним сложение значений в следующем столбце и результат занесем в строку результата 5) Будем повторять шаги 2-4 до тех пор пока будет куда заносить результат умножения. (Последний столбец - столбец со свободным членом делимого.) 6) Просуммируем значения всех оставшихся столбцов и впишем результат в строку результата 7) Отделим частное и остаток. Количество членов остатка будет равно количеству членов делителя за минусом одного. |
Не монический делитель
Алгоритм работает так же и для обычных делителей ( не монических полиномов).
Рассмотрим на примере: 3x3+5x2+7x+2 / 3x2-x-2.
| Алгоритм для не монического делителя | |
|---|---|
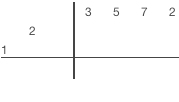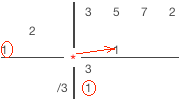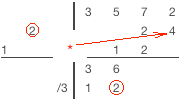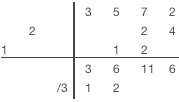 |
1) Опустим старший коэффициент делимого в строку остатка (предпоследняя строка). 2) Поделим последний коэффициент в строке остатка на старший коэффициент делителя, результат запишем в строку результата (последняя строка) 3) Умножим диагональ с коэффициентами делителя на крайний левый коэффициент из строки результатов 4) Поместим результат умножения диагонально справа от последнего столбца с результатами 5) Выполним сложение значений в следующем столбце и результат занесем в строку остатка 6) Повторим шаги 2-5 тех пор пока будет куда заносить результат умножения. (Последний столбец - столбец со свободным членом делимого.) 6) Просуммируем значения всех оставшихся столбцов и впишем результат в строку остатка 7) Отделим частное и остаток. Коэффициенты частного будут в последнем столбце. Коэффициенты остатка - в предпоследнем. Количество членов остатка будет равно количеству членов делителя за минусом одного. |
Ссылка скопирована в буфер обмена
Похожие калькуляторы
PLANETCALC, Синтетическое деление полиномов
Комментарии