Расстояние между двумя координатами сквозь Землю
Этот калькулятор определяет расстояние между двумя точками земной поверхности, заданными координатами, напрямую, "сквозь Землю", в отличие от расстояния по поверхности Земли.
Этот материал распространяется на условиях лицензии Creative Commons Attribution/Share-Alike License 3.0 (Unported). Это означает, что вы можете размещать этот контент на своем сайте или создавать на его основе собственный (в том числе и в коммерческих целях), при условии сохранения оригинального лицензионного соглашения. Кроме того, Вы должны отметить автора этой работы, путем размещения HTML ссылки на оригинал работы https://planetcalc.ru/7725/. Пожалуйста оставьте без изменения все ссылки на других авторов данной работы или работы, на основе которой создана данная работа (если таковые имеются в спроводительном тексте).
Если вы хотите узнать кратчайшее расстояние между двумя точками земной поверхности, вы должны использовать ортодромию. На этом сайте уже есть два калькулятора для этого: один, использующий формулу гаверсинусов, и второй, использующий формулу Винсенти.
Однако, что если вам надо узнать расстояние между двумя точками напрямую, "сквозь Землю", а не по поверхности? В принципе, эта задача решается достаточно просто, за исключением пары тонких моментов. Калькулятор ниже рассчитывает расстояние между двумя точками сквозь Землю, а вывод формулы расчета вы можете найти под калькулятором.
Расстояние сквозь Землю
Итак у нас есть две точки на земной поверхности, заданные широтой и долготой, и мы хотим знать расстояние между ними напрямую, сквозь Землю. Технически, широта и долгота представляют собой часть сферических координат в трехмерном пространстве, а именно: радиус - это радиус Земли, угол наклонения -
это широта, и азимут - это долгота. Если мы преобразуем сферические координаты в декартовы координаты x, y, z, мы сможем с легкостью найти расстояние напрямую между этими точками, используя формулу Евклидова расстояния:
Определимся с нашей декартовой системой координат. Начальной точкой будет центр Земли, ось x будет указывать на точку пересечения нулевого меридиана с плоскостью экватора, ось y будет указывать на точку пересечения меридиана 90 градусов западной долготы с плоскостью экватора, а ось z будет указывать строго на север.
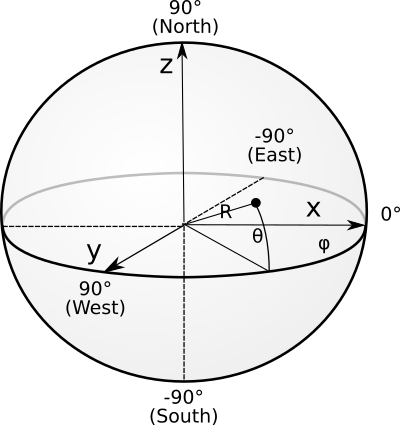
это долгота,
это широта.
Для преобразования сферических координат к декартовым используем следующие формулы:
Теперь пара тонких моментов, которые возникают из-за того факта, что геодезия приближенно представляет форму Земли в виде сплющенного сфероида, или эллипсоида вращения. Поэтому, когда мы говорим о координатах, мы на самом деле говорим о координатах на поверхности референц-эллипсоида используемого в конкретной системе координат, в нашем случае это WGS 84. И рассчитанное расстояние, соответственно, будет расстоянием между двумя точками на поверхности референц-эллипсоида.
Это приводит к необходимости учета следующих факторов:
-
Радиус Земли (радиус эллипсоида) не является постоянной величиной, и зависит от широты рассматриваемой точки. Таким образом мы должны рассчитать значение радиуса для каждой точки отдельно. Это можно сделать используя алгоритм, описанный здесь.
- широта указанная в WGS 84 - это геодезическая широта, которая определяется углом между плоскостью экватора и нормалью к поверхности эллипсоида в данной точке, в отличие от геоцентрической широты, которая определяется углом между экваториальной плоскостью и центром эллипсоида. Так как в нашей декартовой системе координат начало координат находится в центре Земли, мы должны перейти от геодезических координат к геоцентрическим для обеих точек.
Калькулятор учитывает эти факторы, используя следующие формулы для преобразования широты и радиуса:
,
где - геоцентрическая широта,
- геодезическая широта,
- большая полуось референц-эллипсоида,
- малая полуось референц-эллипсоида.
Итак, подводя итог, можно сказать, что для того, чтобы рассчитать растояние напрямую между двумя точками по заданным координатам, надо сделать следующее:
- Рассчитать значение радиуса Земли в каждой точке в зависимости от широты
- Рассчитать геоцентрическую широту в каждой точке
- Перейти от сферических координат к декартовым используя долготу, рассчитанный радиус и рассчитанную геоцентрическую широту.
- Рассчитать расстояние используя формулу Евклидова расстояния
Похожие калькуляторы
- • Радиус Земли по широте (WGS 84)
- • Расстояние между двумя координатами
- • Расстояние по поверхности Земли и расстояние сквозь Землю
- • Путевые углы и расстояние между двумя точками на ортодроме (дуге большого круга).
- • Путевой угол и расстояние между двумя точками по локсодроме (линии румба).
- • Раздел: Навигация ( 9 калькуляторов )
Комментарии