Объем жидкости в наклоненном цилиндрическом баке
Калькулятор вычисляет объем жидкости в бочке правильной цилиндрической формы, лежащей под наклоном. Для вычисления требуется знать размеры емкости, угол наклона и уровень жидкости у одного из оснований.
Продолжая тему, начатую тут Объем жидкости в цилиндрической таре и в ответ на запрос Прошу помочь с расчётом публикуем калькулятор, вычисляющий объем жидкости в цилиндрической емкости под наклоном.
Для вычисления вам потребуется ввести параметры емкости (радиус и длину) замерить уровень жидкости вблизи от одного из оснований и угол наклона.
Замер уровня жидкости
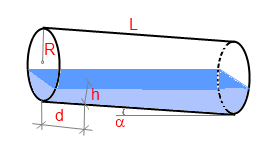
Замер уровня жидкости должен производиться в диаметральной плоскости емкости перпендикулярно нижней цилиндрической стенке (см. рисунок), непосредственно у одного из оснований или на некотором расстоянии от него ( в этом случае надо заполнить параметр «Расстояние от основания при измерении»). Как вариант замера, в случае небольшого количества жидкости и если есть возможность наклонить емкость, можно наклонить ее таким образом, чтобы уровень у верхнего основания был нулевым. Тогда надо замерить только расстояние от верхнего основания до границы начала жидкости. Если же наклонить бочку так, что жидкость будет подходить ровно к верхнему углу (месту смыкания верхнего основания и боковой поверхности емкости) то уровень и расстояние до основания будут нулевыми, замерить потребуется только угол.
Детали и формулы расчета можно найти непосредственно под калькулятором.
Готовой формулы для вычисления объема жидкости в наклонной емкости мне найти не удалось, поэтому пришлось ее выводить.
Если одно основание емкости заполнено полностью, то весь объем жидкости можно условно разделить на две части:
- цилиндрическая часть, объем которой находится тривиально по формуле объема цилиндра см. Цилиндр
- часть цилиндра усеченная под углом поверхностью воды. Объем этой части найти также не трудно по той же формуле, деленной пополам, если жидкость не доходит до верхнего основания (емкость стоит почти вертикально).
Формулы для вычисления объема частично заполненной части емкости
Сложности начинаются, если жидкость частично закрывает одно или оба основания, так как на рисунке.
Для вычисления объема такого тела мы заметим, что любое сечение этого тела перпендикулярно длине емкости представляет собой Сегмент круга. Тогда объем этого тела можно записать, как определенный интеграл по площади сегмента в зависимости от длины фигуры:
где -функция зависимости угла сегмента от длины фигуры x,
которая выражается следующим образом:
где
a — угол наклона емкости,
h0 — уровень жидкости у верхнего основания цилиндра (длина погруженной части верхнего основания) см. раздел Замер уровня жидкости
Подставим в формулу объема это выражение и упростив его получим полную формулу объема:
где
Вычислив интеграл, получаем:
где ,
Определение длины частично заполненной части
Приведенные выше формулы справедливы для следующих предположений:
- Оба основания заполнены частично
- Уровень жидкости h0 измерен непосредственно у верхнего основания с учетом наклона. (Фактически h0 - это длина погруженной части верхнего основания см. раздел Замер уровня жидкости).
- Нет полностью пустых или полностью заполненных частей цилиндра.
Но калькулятор может принимать на вход значения уровня жидкости, измеренные на некотором расстоянии от верхнего либо от нижнего основания. Допускаются полностью пустые и полностью полные части цилиндрической емкости.
Чтобы вычислить уровень жидкости у верхнего основания hu используйте формулы:
где hll - уровень жидкости, измеренный на расстоянии ll от нижнего основания, Lc - длина емкости
где hlu - уровень жидкости, измеренный на расстоянии lu от верхнего основания.
Если уровень huравен или больше нуля, мы считаем h0=hu, и Lf = Lc.
Пустая часть бака
В противном случае hu может быть отрицательным. Это означает, что какая-то часть бака пуста. В этом случае мы полагаем h0=0 и вычисляем длину оставшейся (заполненной) части цилиндра: Lf по формуле:
где Lc - длина цилиндра.
Полностью заполненная часть
Уровень жидкости у нижнего основания h1 можно определить следующим образом:
Если вычисленно значение h1 больше диаметра цилиндра, то некоторая часть цилиндра - заполнена полностью. Чтобы вычислить длину этой части мы используем формул:
Объем этой части посчитать тривиально: Цилиндр
После этих вычислений мы можем подставить длину частично заполненной части и уровень жидкости h0 в формулы первого раздела, чтобы вычислить объем.
Комментарии