Расчет расхода жидкости при ее истечении из отверстия при постоянном напоре.
Этот онлайн калькулятор рассчитывает расход жидкости при ее истечении через малое отверстие в тонкой стенке при постоянном уровне (напоре) жидкости в резервуаре.
Эта страница существует благодаря следующим персонам
 | Timur
|
Этот материал распространяется на условиях лицензии Creative Commons Attribution/Share-Alike License 3.0 (Unported). Это означает, что вы можете размещать этот контент на своем сайте или создавать на его основе собственный (в том числе и в коммерческих целях), при условии сохранения оригинального лицензионного соглашения. Кроме того, Вы должны отметить автора этой работы, путем размещения HTML ссылки на оригинал работы https://planetcalc.ru/10357/. Пожалуйста оставьте без изменения все ссылки на других авторов данной работы или работы, на основе которой создана данная работа (если таковые имеются в спроводительном тексте).
Отметим, что согласно учебнику Кудинова и Карташова1 ($8.1), cтенка считается тонкой , если ее толщина меньше 0.2d, где d – диаметр отверстия. Отверстие считается малым, если площадь сечения отверстия не больше чем 0.1ω1, где ω1 - площадь поперечного сечения сосуда. Также в формуле участвует коэффициент расхода - для малых круглых отверстий в тонкой стенке коэффициент расхода в среднем равен 0.60 - 0.62. Подробнее о формуле расчета и различных значениях коэффициента расхода можно прочитать под калькулятором.
Расчет расхода жидкости при ее истечении из отверстия при постоянном напоре.
Истечение через малое отверстие в тонкой стенке
В случае истечения жидкости через отверстие, нас в первую очередь интересует расход вытекающей жидкости. Расход жидкости, в свою очередь, определяется скоростью истечения - как произведение, собственно, скорости истечения жидкости, на площадь сечения отверстия. В случае идеальной жидкости (жидкости, в которой отсутствует вязкость и теплопроводность) скорость истечения определяется формулой Торричелли
где g - ускорение свободного падения, h - высота напора, или высота уровня жидкости над центром тяжести незатопленного отверстия.
И расход идеальной жидкости Q равен
где ω - площадь сечения отверстия.
Для реальной жидкости в формулу Торричелли вводится коэффициент скорости ϕ, зависящий от коэффициента гидравлического сопротивления при входе в отверстие
А в формулу расхода жидкости - коэффициент сжатия струи α, т.е. отношения площади сжатого сечения струи к площади отверстия, см. рисунок ниже.
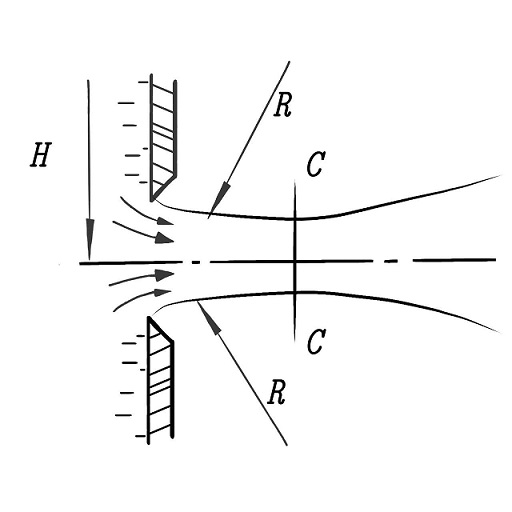
Сжатие струи обуславливается инерцией частиц жидкости, движущихся при подходе к отверстию по криволинейным траекториям2 ($4.9).
Произведение значений α и ϕ и называют коэффициентом расхода μ
Для вязких жидкостей и низких скоростей истечения коэффициенты α, ϕ и, следовательно, μ будут зависеть от числа Рейнольдса.
Число Рейнольдса характеризует отношение инерционных сил к силам вязкого трения в вязких жидкостях и газах, и вычисляется через плотность среды, характерную скорость, гидравлический диаметр и динамическую вязкость среды. Для каждого вида потока существует некоторое критическое значение числа Рейнольдса, до которого поток характеризуется ламинарным течением, т.е. жидкость или газ перемещаются слоями без перемешивания и пульсаций, при переходе через которое течение становится неустойчиво турбулентным, а при дальнейшем увеличении числа Рейнольдса потока - устойчиво турбулентным.
При больших числах Рейнольдса (>104, турбулентный режим) коэффициенты истечения постоянны, зависят только от вида отверстия, определяются опытным путем и приводятся в справочниках.
Например, справочник Зиновьева3 (6. Гидромеханика, табл.24) приводит следующие значения коэффициента расхода μ:
| Вид отверстий и характер истечения жидкости | μ |
|---|---|
| Малые отверстия с полным сжатием | 0.6 |
| Отверстия средних размеров со сжатием струи со всех сторон (при отсутствии направляющих стенок) в среднем | 0.65 |
| Отверстия в вертикальной стенке непосредственно у дна со значительным влиянием бокового сжатия, но вовсе не имеющие сжатия по дну | 0.65 - 0.70 |
| То же, но с умеренным влиянием бокового сжатия | 0.70 - 0.75 |
| То же с плавными боковыми подходами | 0.80 - 0.85 |
Повлиять на коэффициент расхода можно насадками. Насадком называется короткая труба, длиной от 3 до 5 диаметров отверстия, подсоединенная к отверстию. Так, например, цилиндрический насадок образует водоворотную зону на входе и снижает коэффициент скорости. Конический сходящийся насадок позволяет добиться коэффициента расхода 0.95, конический расходящийся - 0.47 (зависит от угла), коноидальный - 0.98! Для расчетов, естественно, берется сечение на выходе из насадка.
-
Кудинов В.А., Карташов Э.М. Гидравлика. Учеб. пособие для втузов. М.: Высш. шк., 2004.– 180 с.: ил. ↩
-
Курс лекций по дисциплине «Гидравлика» для студентов строительных специальностей очной формы обучения (технология 30/70) / Составитель Калинин А.В., Лушкин И.А. – Тольятти: ТГУ, 2007. ↩
-
Краткий технический справочник под общей редакцией Вяч. А. Зиновьева. Часть первая. Москва Ленинград: Государственное издательство технико-теоретической литературы, 1949 ↩
Комментарии