Продолжаем серию калькуляторов про матрицы, предыдущие калькуляторы: Определитель (детерминант) матрицы, Транспонирование матрицы, Умножение матриц.

Калькулятор ниже находит обратную матрицу с помощью метода Гаусса-Жордана. Раньше он вычислял обратную матрицу через союзную матрицу, но данный способ подходит только для матриц небольшого размера. Немного теории, как водится, под калькулятором.

Обратная матрицаCreative Commons Attribution/Share-Alike License 3.0 (Unported)
0.12345678901234567890
Рассчитать

Итак, обратная матрица — такая матрица, при умножении на которую исходная матрица A даёт в результате единичную матрицу E:
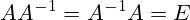
AA^{-1} = A^{-1}A = E

В данном калькуляторе используется способ нахождения обратной матрицы через союзную матрицу по формуле:
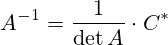
A^{-1} = \frac{1}{\det A}\cdot C^*

Союзная матрица - матрица, составленная из алгебраических дополнений для соответствующих элементов транспонированной матрицы.
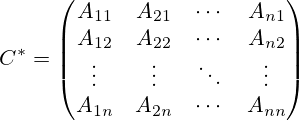
{C}^{*}= \begin{pmatrix} {A}_{11} & {A}_{21} & \cdots & {A}_{n1} \\ {A}_{12} & {A}_{22} & \cdots & {A}_{n2} \\ \vdots & \vdots & \ddots & \vdots \\ {A}_{1n} & {A}_{2n} & \cdots & {A}_{nn} \\ \end{pmatrix}

Ну и чтобы два раза не ходить —
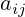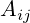
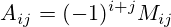
Алгебраическое дополнение элемента a_{ij} матрицы A это число A_{ij}A_{ij}=(-1)^{i+j}M_{ij}
где 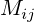M_{ij} — определитель матрицы, получающейся из исходной матрицы A путем вычёркивания i -й строки и j -го столбца (дополнительный минор).