Скорость и длина волны
Расчет по уравнению скорости и длины волны.
Эта страница существует благодаря следующим персонам
 | Timur
|
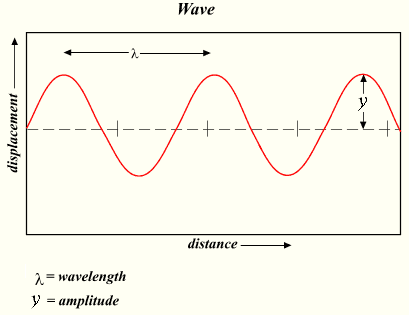
Если бросить камень в воду, то в месте его падения частицы воды начинают колебаться, двигаясь вверх и вниз. Соседние частицы, связанные с ними силами сцепления, также приходят в колебание. Однако для передачи колебания соседним частицам требуется некоторое время. То есть, чем дальше отстоят частицы от места, где начались колебания, тем позже эти частицы будут вовлечены в колебательное движение. Таким образом, от места падения камня волна бежит во все стороны с определенной скоростью, которая называется скоростью распространения волны. Длиной волны называется расстояние, на которое распространяется волна за время, равное периоду колебаний в ней. Если считать скорость волны постоянной, то пройденное волной расстояние равно произведению скорости на время ее распространения. Таким образом, чтобы найти длину волны, надо скорость волны умножить на период колебаний в ней:
Так как период колебаний в волне обратно пропорционален частоте,
,
то можно получить формулу, выражающую связь длины волны с ее скоростью и частотой:
Калькулятор ниже позволяет по двум известным параметрам формулы посчитать неизвестный.
Комментарии