PLANETCALC Онлайн калькуляторы

Войти
УчебаМатематикаГеометрия

Площадь четырехугольной пирамиды

Этот онлайн калькулятор находит площадь поверхности четырехугольной пирамиды, в основании которой лежит прямоугольник через длины сторон основания и один из следующих параметров: длину ребра, угол наклона граней, высоту пирамиды.

Формулы для расчета приведены под калькулятором.

PLANETCALC, Площадь четырехугольной пирамиды

Площадь четырехугольной пирамиды

°
′
″
Площадь основания
 
Площадь боковых граней
 
Общая площадь
 
Знаков после запятой: 2

Четырехугольная пирамида

В формулах ниже будем использовать следующие обозначения:
a - длина первой стороны основания
b - длина второй стороны основания (для квадрата будет равна первой)
h - высота пирамиды
r - ребро пирамиды
d - диагональ основания
e - высота треугольника, образованного боковой гранью, т.е. высота, опущенная из вершины пирамиды на ее сторону
α - угол наклона грани пирамиды (угол между высотой треугольника боковой грани и плоскостью основания)

pyramid1.png



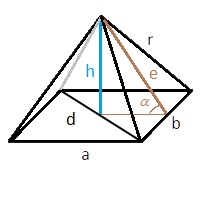
Во всех случаях площадь основания вычисляется тривиально - перемножением длин сторон основания. Ниже рассмотрим нахождение площадей боковых граней для разных случаев.

Площадь поверхности пирамиды через высоту

  1. Находим высоту треугольника, образованного боковой гранью. Используем теорему Пифагора на прямоугольном треугольнике, образованном высотой пирамиды, высотой треугольника боковой грани, и проекцией высоты треугольника на плоскость основания. Длина проекции очевидно равна половине длины противоположной стороны. Таким образом, высота треугольника, опущенная на сторону a
    e_a=\sqrt{h^2+\frac{b^2}{4}}
    высота треугольника, опущенная на сторону b
    e_b=\sqrt{h^2+\frac{a^2}{4}}

  2. Находим площади боковых граней, по формуле площади равнобедренного треугольника
    S_a=\frac{a\cdot e_a}{2}\\S_b=\frac{b\cdot e_b}{2}

  3. Общая площадь боковых граней
    S=2S_a+2S_b

Площадь поверхности пирамиды через угол наклона

Расчет через один угол наклона возможен, только если в основании пирамиды лежит квадрат (иначе пришлось бы задавать два угла). Соответственно, сторона a равна стороне b, и все грани одинаковые.

  1. Находим высоту треугольника, образованного боковой гранью, поделив длину проекции на плоскость основания на косинус угла наклона
    e=\frac{\frac{a}{2}}{cos \alpha}

  2. Находим площадь боковой грани, по формуле площади равнобедренного треугольника
    S=\frac{a\cdot e}{2}

  3. Общую площадь боковых граней получаем, умножив площадь одной грани на 4.

Площадь поверхности пирамиды через длину ребра

Здесь есть ограничение: длина ребра должна быть больше чем половина диагонали основания (иначе это не пирамида)

  1. Находим высоту треугольника, образованного боковой гранью. Используем теорему Пифагора на прямоугольном треугольнике, образованном ребром пирамиды, высотой треугольника боковой грани, и половиной стороны, на которую опущена высота. Таким образом, высота треугольника, опущенная на сторону a
    e_a=\sqrt{r^2-\frac{a^2}{4}}
    высота треугольника, опущенная на сторону b
    e_b=\sqrt{r^2-\frac{b^2}{4}}

  2. Находим площади боковых граней, по формуле площади равнобедренного треугольника
    S_a=\frac{a\cdot e_a}{2}\\S_b=\frac{b\cdot e_b}{2}

  3. Общая площадь боковых граней
    S=2S_a+2S_b
Ссылка скопирована в буфер обмена

Похожие калькуляторы

 Геометрия Математика
PLANETCALC, Площадь четырехугольной пирамиды
Timur2022-12-01 07:18:16

Комментарии