Поле не заполнено.

'%1' не похож на адрес электронной почты.

Пожалуйста, заполните это поле.

Значение поля должно содержать как минимум %1 символов.

Значение не должно быть длиннее %1 символов.

Значение поля не совпадает с полем '%1'

Введен неверный символ. Допустимые символы:'%1'.

Ожидается число.

Ожидается положительное число.

Ожидается целое число.

Ожидается положительное целое число.

Значение должно быть в диапазоне [%1 .. %2]

Символ '%1' уже присутствует в наборе допустимых символов.

Значение поля должно быть меньше %1.

Первым символом должна быть буква латинского алфавита.

Вс

Пн

Вт

Ср

Чт

Пт

Сб

Январь

Февраль

Март

Апрель

Май

Июнь

Июль

Август

Сентябрь

Октябрь

Ноябрь

Декабрь

век

до Н.Э.

Возникла ошибка при импорте данных в строке:%1. Значение: '%2'. Ошибка: %3

Невозможно определить разделитель полей. Для разделения полей можно использовать следующие символы: Tab, точку с запятой (;) или запятую (,).

%3.%2.%1%4

%3.%2.%1%4 %6:%7

с.ш.

ю.ш.

в.д.

з.д.

да

нет

Неправильный формат файла. Поддерживаются только следующие форматы: %1

минут

минута

минуты

минут

час

часа

часов

дней

день

дня

дней

месяц

месяца

месяцев

год

года

лет

Создан 2009-03-23 18:36:08
пользователем Anton

Онлайн калькулятор: Тригонометрические функции

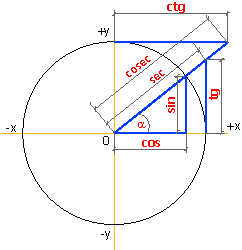
Тригонометрические функции - вид элементарных функций, к которым относятся следующие функции:
sin - синус
cos - косинус
tg - тангенс
ctg - котангенс
sec - секанс
cosec - косеканс
versin - версинус (синус-верзус)
vercos - коверсинус (косинус-верзус)
haversin - гаверсинус (половина от синус-верзус)
exsec - экссеканс
excsc - экскосеканс

Для того, чтобы вычислить все эти тригонометрические функции сразу для заданного угла, введите значение угла в поле Угол и получите результат в виде таблицы значений всех функций для этого угла. Угол можно задать в градусах, радианах, градах, минутах и секундах, для выбора единицы измерения - просто щелкните на ее название.

Тригонометрические функции

Угол:
Единицы измерения: Градусы Радианы Грады Минуты Секунды
Точность вычисления:
0.1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0
Рассчитать
1. Значение тригонометрических функций:
Установить на ваш мобильный телефон

Как известно из школы, синус угла ( sin )- это отношение длины противоположного этому углу катета к гипотенузе, а косинус ( cos )- это отношение прилежащего этому углу катета к гипотенузе.

Остальные тригонометрические функции можно выразить через синус и косинус:
Тангенс: $\operatorname{tg}\alpha=\frac{\sin\alpha}{\cos\alpha}$ (отношение длины противоположного углу катета к прилежащему катету)
Котангенс: $\operatorname{ctg}\alpha=\frac{\cos\alpha}{\sin\alpha}$ (отношение длины прилежащего к углу катета к противоположному катету)
Секанс: $\operatorname{sec}\alpha=\frac{1}{\cos\alpha}$ (отношение длины гипотенузы к прилежащему к углу катету )
Косеканс: $\operatorname{cosec}\alpha=\frac{1}{\sin\alpha}$ (отношение длины гипотенузы к противоположному катету )

Редко используемые тригонометрические функции:

Версинус: $\operatorname{versin}\alpha=1 - {\cos\alpha}$

Коверсинус: $\operatorname{coversin}\alpha=1 - {\sin\alpha}$

Гаверсинус: $\operatorname{haversin}\alpha=\frac{\operatorname{versin}\alpha}{2}$

Экссеканс: $\operatorname{exsec}\alpha=\operatorname{sec}\alpha -1$

Экскосеканс: $\operatorname{excsc}\alpha=\operatorname{cosec}\alpha -1$

Онлайн калькулятор: Тригонометрические функции

Комментарии

Калькуляторы на эту тему

О нас

Калькуляторы

Сообщество

Персональный раздел