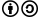Для решения системы уравнений вида
\left{ax+by+cz=d\\a_1x+b_1y+c_1z=d_1\\a_2x+b_2y+c_2z=d_2
существуют общие формулы для нахождения x, y, z. Поскольку в развернутом виде формулы очень громоздки, принято обозначать их через введение понятия определителя или детерминанта третьего порядка, как
\left|\begin{matrix} a & b & c \\ a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \end{matrix} \right| = ab_1c_2 + bc_1a_2 + ca_1b_2 - cb_1a_2 - ac_1b_2 - ba_1c_2
Тогда решение уравнений можно представить в виде
x=\frac{\left|\begin{matrix} d & b & c \\ d_1 & b_1 & c_1 \\ d_2 & b_2 & c_2 \end{matrix} \right|}{\left|\begin{matrix} a & b & c \\ a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \end{matrix} \right|}\\y=\frac{\left|\begin{matrix} a & d & c \\ a_1 & d_1 & c_1 \\ a_2 & d_2 & c_2 \end{matrix} \right|}{\left|\begin{matrix} a & b & c \\ a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \end{matrix} \right|}\\z=\frac{\left|\begin{matrix} a & b & d \\ a_1 & b_1 & d_1 \\ a_2 & b_2 & d_2 \end{matrix} \right|}{\left|\begin{matrix} a & b & c \\ a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \end{matrix} \right|}
т.е. каждое из неизвестных равно дроби, знаменатель которой есть определитель, составленный из коэффициентов при неизвестных, а числитель получается из этого определителя заменой коэффициентов при соответствующем неизвестном на свободные члены.

Решение системы сводится к трем случаям

  1. Определитель, стоящий в знаменателе формул (составленный из коэффициентов при неизвестных) не равен нулю
    \left|\begin{matrix} a & b & c \\ a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \end{matrix} \right|<>0
    тогда система уравнений имеет единственное решение соответствующее формулам выше

  2. Определитель, стоящий в знаменателе формул (составленный из коэффициентов при неизвестных) равен нулю, но ни один из определителей в числителе не равен нулю

    \left|\begin{matrix} a & b & c \\ a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \end{matrix} \right|=0\\\left|\begin{matrix} d & b & c \\ d_1 & b_1 & c_1 \\ d_2 & b_2 & c_2 \end{matrix} \right|<>0\\\left|\begin{matrix} a & d & c \\ a_1 & d_1 & c_1 \\ a_2 & d_2 & c_2 \end{matrix} \right|<>0\\\left|\begin{matrix} a & b & d \\ a_1 & b_1 & d_1 \\ a_2 & b_2 & d_2 \end{matrix} \right|<>0

    тогда система уравнений не имеет решений, потому что уравнения друг другу противоречат

  3. Определитель, стоящий в знаменателе формул (составленный из коэффициентов при неизвестных) равен нулю, определители в числителе также равны нулю \left|\begin{matrix} a & b & c \\ a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \end{matrix} \right|=0\\\left|\begin{matrix} d & b & c \\ d_1 & b_1 & c_1 \\ d_2 & b_2 & c_2 \end{matrix} \right|=0\\\left|\begin{matrix} a & d & c \\ a_1 & d_1 & c_1 \\ a_2 & d_2 & c_2 \end{matrix} \right|=0\\\left|\begin{matrix} a & b & d \\ a_1 & b_1 & d_1 \\ a_2 & b_2 & d_2 \end{matrix} \right|=0

    тогда система уравнений имеет бесчисленное множество решений, потому что одно из уравнений есть следствие двух других

Калькулятор:

Решение системы трех уравнений первой степени с тремя неизвестнымиCreative Commons Attribution/Share-Alike License 3.0 (Unported)
0.12345678901234567890
Рассчитать