Опорные реакции простой балки
Калькулятор вычисляет опорные реакции балки на двух опорах при действии вертикальных нагрузок.
Данный онлайн калькулятор предназначен для нахождения опорных реакций в простейшей балке, находящейся под воздействием поперечных сил. Простая балка - прямолинейный брус, закрепленная на двух опорах: одной - шарнирно-неподвижной (опора А), другой - шарнирно-подвижной (опора В). Калькулятор выводит опорные реакции VA и VB, уравнения равновесия в символьном виде и показывает модель нагрузок. Обратите внимание, что если требуется задать нагрузку действующую левее опоры A, то расстояние от опоры нужно задать со знаком минус. Теорию и формулы расчета можно найти ниже под калькулятором.
Нагрузка
| Расстояние от опоры A | Нагрузка | Значение | Направление | Направление момента | Протяженность | Изменение | ||
|---|---|---|---|---|---|---|---|---|
Реакции опор
Под воздействием нагрузок в опорах балки возникают уравновешивающие силы, называемые реакциями опор. Эти силы зависят от вида нагрузки и типа самих опор.
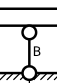
Шарнирно подвижная опора ( в нашей модели обозначена как "B") позволяет балке свободно перемещаться в горизонтальной плоскости и препятствует вертикальному перемещению, поэтому при любой нагрузке она имеет только вертикальную реакцию VB.
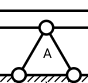
Шарнирно неподвижная опора крепится к балке, что препятствует её горизонтальному и вертикальному перемещению. При наличии сил, действующих на балку в горизонтальной плоскости, эта опора дает еще и горизонтальную реакцию. Однако в нашей модели все силы действуют поперечно балке, поэтому горизонтальная реакция опоры A всегда будет равна нулю. Вертикальную реакцию опоры A обозначим VA.
Уравнения равновесия
Как мы знаем из статики, все силы и моменты сил в неподвижной системе, уравновешены. Поэтому суммы сил и моментов в любой точке этой системы равны нулю.
Все силы при поперечной нагрузке на простую балку действуют параллельно оси Y, поэтому можно составить только два независимых уравнения равновесия для проекции сил и моментов на ось Y. Этого вполне достаточно для нахождения двух неизвестных реакций опор VA и VB.
При составлении уравнений у нас есть выбор:
- составить одно уравнение равновесия проекции сил и одно уравнение равновесия моментов в некоторой точке
- составить два уравнения равновесия моментов в двух точках.
Воспользуемся вторым способом, а первый оставим для проверки полученного результата.
Удобнее всего составлять уравнения для точек А и B, в которых находятся опоры:
Напомним, что моментом силы в определенной точке называется произведение силы F на кратчайшее расстояние от этой точки до линии действия силы (плечо) l:
Исходя из этого, уравнения равновесия моментов в точках А и B для системы поперечных сил F1...Fn, действующих на балку приобретают вид:
Где Fi - модуль приложенной силы или реакции опоры в Ньютонах. liA и liB - длина рычага в метрах (кратчайшее расстояние от точки приложения силы i до опоры A и B соответственно). siA и siB - знак момента силы i в точке A и B соответственно.
Правило выбора знаков момента сил: знак положительный (+1) для момента, закручивающего балку вокруг выбранной точки по часовой стрелке ↻ и отрицательный (-1) для противоположного направления ↺. Можно выбрать и противоположные значения. Уравнения примут немного другой вид, но результат от этого не изменится.
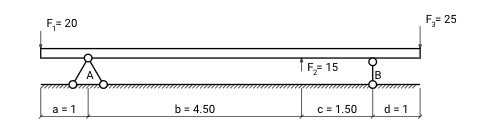
Например, для системы сил, показанной на рисунке выше, уравнения равновесия можно записать следующим образом:
Вычисляя, получаем значения реакций опор: VA = 15.42 и VB = 14.58. Проверим, что сумма всех сил равна нулю (для сил действующих вниз - знак положительный, для действующих вверх - отрицательный):
Составляя уравнения, мы исходили из того, что реакции обеих опор направлены вверх. При расчетах может получиться так, что реакция опоры окажется отрицательной. Это означает, что реакция такой опоры направлена вниз (сумма моментов сил, действующих на балку, пытается оторвать её от опоры).
Распределенная нагрузка
В расчетах, иногда требуется задать нагрузку, которая распределена определенным образом по участку длины a. Для вычисления реакций опор такую нагрузку можно заменить её равнодействующей силой. Точкой приложения такой силы считается центр масс распределенной нагрузки, а модуль вычисляется как интеграл от функции распределения нагрузки на заданном участке. Для простых функций модуль легко выразить через заданную интенсивность нагрузки.
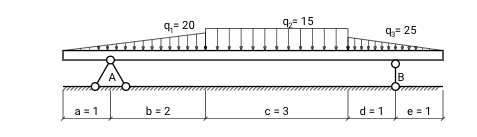
В таблице ниже представлены формулы для модуля сосредоточенной равнодействующей силы и точек её приложения для всех видов распределенных нагрузок, поддерживаемых калькулятором:
| Нагрузка | Модуль | Точка приложения |
|---|---|---|
| Равномерная | 1/2 a | |
| Линейно убывающая | 1/3 a | |
| Линейно возрастающая | 2/3 a |
В формулах q - это интенсивность нагрузки в Н/м, a - диапазон действия распределенной нагрузки, точка приложения силы отсчитывается от начала диапазона действия распределенной нагрузки. Интенсивность для линейно распределенной нагрузки задается для участка максимума нагрузки ( полагаем, что в точке минимума, интенсивность = 0).
После вычисления модуля и плеча равнодействующей распределенной нагрузки их можно подставить в уравнения моментов, точно так же, как мы это делали с сосредоточенными силами.
Сосредоточенный момент
Еще один способ задания нагрузки в калькуляторе - при помощи момента в Нм, приложенного к некоторой точке. Значение сосредоточенного момента добавляется к уравнениям равновесия со знаком, определяемым направлением момента в соответствии с правилом знаков. Точка приложения сосредоточенного момента для вычисления реакций опор в простой балке значения не имеет.
Комментарии