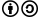Факториал числа n (обозначается n!) — произведение всех натуральных чисел до n включительно:
n! = 1\cdot 2\cdot\ldots\cdot n =\prod_{i=1}^n i
По определению полагают 0! = 1. Факториал определён только для целых неотрицательных чисел.

Поскольку в вычислениях иногда бывает довольно трудно перемножать все числа входящие в факториал, используется так называемая формула Стирлинга:
n! = \sqrt{2\pi n}\left(\frac{n}{e}\right)^n \left(1 + \frac{1}{12 n} + \frac{1}{288 n^2} - \frac{139}{51840 n^3}+O\left(n^{-4}\right)\right)
приближенная формула для вычисления факториала.

Во многих случаях для упрощения рассматривают только главный член формулы
n! \approx \sqrt{2\pi n}\left(\frac{n}{e}\right)^n

При этом утверждается, что
\sqrt{2\pi n}\left(\frac{n}{e}\right)^n < n! < \sqrt{2\pi n}\left(\frac{n}{e}\right)^n e^{1/(12n)}

Калькулятор рассчитывает "честный" факториал, факториал по формуле Стирлинга, а также нижнюю и верхнюю границу (из неравенства). К сожалению, из-за ограниченных вычислительных способностей Javascript максимально возможный факториал для калькулятора — 170!

ФакториалCreative Commons Attribution/Share-Alike License 3.0 (Unported)
0.12345678901234567890
Рассчитать